Ley de Ampère
De Laplace
(Diferencias entre revisiones)
(→Demostración) |
(→Límites de validez) |
||
| Línea 16: | Línea 16: | ||
==Límites de validez== | ==Límites de validez== | ||
| + | A diferencia de la Ley de Gauss para el campo magnético, la ley de Ampère ''sólo'' es válida para ''corrientes estacionarias''. Deberá ser odificada cuando existan campos o corrientes variables en el tiempo. | ||
| + | |||
==Forma integral== | ==Forma integral== | ||
==Condición de salto== | ==Condición de salto== | ||
==La ley de Ampère-Maxwell== | ==La ley de Ampère-Maxwell== | ||
Revisión de 18:55 21 mar 2009
Contenido |
1 Forma diferencial
El rotacional del campo magnético puede calcularse igualmente a partir de la ley de Biot y Savart para una densidad de corriente de volumen. El resultado es la llamada Ley de Ampère (descubierta por Maxwell):
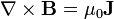
1.1 Demostración
Para demostrar esta ley partiendo de la ley de Biot y Savart se aplica que
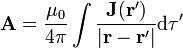
Aplicando que
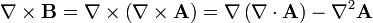
resultan dos expresiones integrales. La primera se anula demostrando que este campo 
es solenoidal (lo cual no es trivial). La segunda, tras aplicar las propiedades de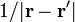 
resulta ser igual a 
.
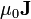2 Límites de validez
A diferencia de la Ley de Gauss para el campo magnético, la ley de Ampère sólo es válida para corrientes estacionarias. Deberá ser odificada cuando existan campos o corrientes variables en el tiempo.
