Teorema de Gauss
De Laplace
(Diferencias entre revisiones)
(Nueva página: El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss <center><math>\oint_{\partial\tau} \mathbf{...) |
|||
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss | El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss | ||
| Línea 5: | Línea 6: | ||
que nos dice que la cantidad de campo que escapa hacia el exterior de una superficie cerrada <math>\partial\tau</math> es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie. | que nos dice que la cantidad de campo que escapa hacia el exterior de una superficie cerrada <math>\partial\tau</math> es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie. | ||
| + | ==Demostración== | ||
| + | |||
| + | ==Aplicaciones== | ||
[[Categoría:Fundamentos matemáticos]] | [[Categoría:Fundamentos matemáticos]] | ||
última version al 17:16 21 mar 2009
1 Enunciado
El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss
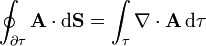
que nos dice que la cantidad de campo que escapa hacia el exterior de una superficie cerrada 
es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie.
