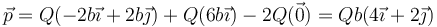Entrar Página Discusión Historial Go to the site toolbox

Tres superficies esféricas cargadas (GIE)

De Laplace

(Diferencias entre revisiones)
(→Potencial eléctrico)
Línea 59: Línea 59:
El potencial eléctrico se calcula de forma similar. Para una superficie esférica el potencial es de la forma
El potencial eléctrico se calcula de forma similar. Para una superficie esférica el potencial es de la forma
-
<center><math>V=\begin{cases}\dfrac{Q}{4\pi\varepsilon_0R} & (r<R) \\ & \\ \dfrac{Q}{4\pi\varepsilon_0R} & (r\geq R)\end{cases}</math></center>
+
<center><math>V=\begin{cases}\dfrac{Q}{4\pi\varepsilon_0R} & (r<R) \\ & \\ \dfrac{Q}{4\pi\varepsilon_0r} & (r\geq R)\end{cases}</math></center>
siendo r la distancia al centro de la esfera y R el radio de ésta. Aplicando esta expresión a cada caso resulta
siendo r la distancia al centro de la esfera y R el radio de ésta. Aplicando esta expresión a cada caso resulta

Revisión de 16:05 8 abr 2021

Contenido

1 Enunciado

Suponga un sistema formado por tres superficies esféricas cargadas uniformemente. Una de ellas posee una carga + Q y radio 4b, estando centrada en 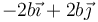-2b\vec{\imath}+2b\vec{\jmath}. La segunda posee también carga + Q y radio b, estando centrada en 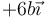+6b\vec{\imath}. La tercera envuelve a las otras dos, almacena una carga − 2Q, posee radio 8b y está centrada en el origen de coordenadas.

  1. Determine el valor del campo eléctrico en los puntos del plano OXY: O(0,0), A(6b,2b), B( − 2b, − 6b), C(6b,8b) y D(2b,b)
  2. Halle el valor del potencial eléctrico en los mismos puntos, tomando como origen de potencial el infinito.
  3. Calcule el trabajo necesario para mover una carga puntual q desde el punto A al punto B siguiendo el camino rectilíneo indicado en la figura.
  4. En puntos exteriores muy alejados el sistema se ve como un dipolo. ¿Cuánto vale el momento dipolar de esta distribución de cargas?
Error al crear miniatura:

2 Campo eléctrico

El campo debido a una superficie esférica cargada uniformemente cumple:

  • En el interior de la esfera es nulo.
  • En el exterior equivale a que toda la carga estuviera concentrada en el centro de la esfera.

El campo de una carga puntual es

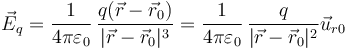
\vec{E}_q=\frac{1}{4\pi\varepsilon_0}\,\frac{q(\vec{r}-\vec{r}_0)}{|\vec{r}-\vec{r}_0|^3}=\frac{1}{4\pi\varepsilon_0}\,\frac{q}{|\vec{r}-\vec{r}_0|^2}\vec{u}_{r0}

siendo 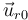\vec{u}_{r0} el unitario radial desde la carga hasta el punto donde se halla el campo.

Al tener tres esferas, el campo en cada punto será la suma de los campos debidos a cada una de ellas.

2.1 Punto O

O está dentro de la esfera 1 y la 3, y fuera de la 2.

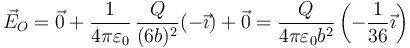
\vec{E}_O=\vec{0}+\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{(6b)^2}(-\vec{\imath})+\vec{0}=\frac{Q}{4\pi\varepsilon_0 b^2}\left(-\frac{1}{36}\vec{\imath}\right)

2.2 Punto A

A está fuera de la 1 y de la 2 y dentro de la 3

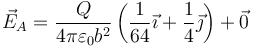
\vec{E}_A=\frac{Q}{4\pi\varepsilon_0b^2}\left(\frac{1}{64}\vec{\imath}+\frac{1}{4}\vec{\jmath}\right)+\vec{0}

2.3 Punto B

A está fuera de la 1 y de la 2 y dentro de la 3

\vec{E}_B=\frac{Q}{4\pi\varepsilon_0b^2}\left(-\frac{1}{64}\vec{\jmath}+\left(\frac{-8\vec{\imath}-6\vec{\jmath}}{1000}\right)\right)+\vec{0}=\frac{Q}{4\pi\varepsilon_0b^2}\frac{(-64\vec{\imath}-173\vec{\jmath})}{8000}

2.4 Punto C

Está fuera de las tres esferas

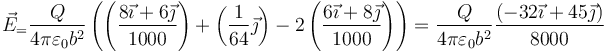
\vec{E}_=\frac{Q}{4\pi\varepsilon_0b^2} \left( \left( \frac{8\vec{\imath}+6\vec{\jmath}}{1000} \right) + \left( \frac{1}{64}\vec{\jmath} \right) -2\left( \frac{6\vec{\imath}+8\vec{\jmath}}{1000} \right) \right) =\frac{Q}{4\pi\varepsilon_0b^2}\frac{(-32\vec{\imath}+45\vec{\jmath})}{8000}

2.5 Punto D

También está dentro de 3 y fuera de 1 y 2. En este punto se ve el campo de dos cargas +Q, pero al ser D el punto medio entre estas dos cargas

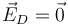
\vec{E}_D=\vec{0}

3 Potencial eléctrico

El potencial eléctrico se calcula de forma similar. Para una superficie esférica el potencial es de la forma

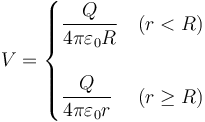
V=\begin{cases}\dfrac{Q}{4\pi\varepsilon_0R} & (r<R) \\ & \\ \dfrac{Q}{4\pi\varepsilon_0r} & (r\geq R)\end{cases}

siendo r la distancia al centro de la esfera y R el radio de ésta. Aplicando esta expresión a cada caso resulta

3.1 Punto O

O está dentro de la esfera 1 y la 3, y fuera de la 2.

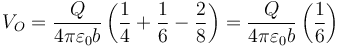
V_O=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{4}+\frac{1}{6}-\frac{2}{8}\right)=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{6}\right)

3.2 Punto A

A está fuera de la 1 y de la 2 y dentro de la 3

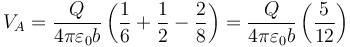
V_A=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{6}+\frac{1}{2}-\frac{2}{8}\right)=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{5}{12}\right)

3.3 Punto B

A está fuera de la 1 y de la 2 y dentro de la 3

V_B=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{8}+\frac{1}{10}-\frac{2}{8}\right)=\frac{Q}{4\pi\varepsilon_0b}\left(-\frac{1}{40}\right)

3.4 Punto C

Está fuera de las tres esferas

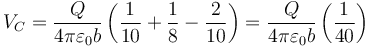
V_C=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{10}+\frac{1}{8}-\frac{2}{10}\right)=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{40}\right)

3.5 Punto D

También está dentro de 3 y fuera de 1 y 2.

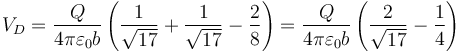
V_D=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{1}{\sqrt{17}}+\frac{1}{\sqrt{17}}-\frac{2}{8}\right)=\frac{Q}{4\pi\varepsilon_0b}\left(\frac{2}{\sqrt{17}}-\frac{1}{4}\right)

4 Trabajo

El trabajo para mover la carga entre los dos puntos es independiente del camino e igual a

W=q(V_B-V_A)=\frac{qQ}{4\pi\varepsilon_0b}\left(-\frac{1}{40}-\frac{5}{12}\right)=-\frac{qQ}{4\pi\varepsilon_0b}\left(\frac{53}{120}\right)

5 Momento dipolar

Desde el exterior vemos tres cargas puntuales situadas en los centros respectivos, por lo que el momento dipolar es

\vec{p}=Q(-2b\vec{\imath}+2b\vec{\jmath})+Q(6b\vec{\imath})-2Q(\vec{0})=Qb(4\vec{\imath}+2\vec{\jmath})
Obtenido de "http://tesla.us.es/wiki/index.php/Tres_superficies_esf%C3%A9ricas_cargadas_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace