Cinética de un cono (CMR)
De Laplace
(→En el sistema intermedio) |
|||
| Línea 131: | Línea 131: | ||
con la matriz de rotación | con la matriz de rotación | ||
| - | <center><math>\bar{\bar{R}}=\begin{pmatrix}1 & 0 & 0 \\ 0 & C & -S \\ 0 & S & C\end{pmatrix}=\frac{1}{\sqrt{R^2+H^2}}begin{pmatrix}1 & 0 & 0 \\ 0 & H & -R \\ 0 & R & H\end{pmatrix}</math></center> | + | <center><math>\bar{\bar{R}}=\begin{pmatrix}1 & 0 & 0 \\ 0 & C & -S \\ 0 & S & C\end{pmatrix}=\frac{1}{\sqrt{R^2+H^2}}\begin{pmatrix}1 & 0 & 0 \\ 0 & H & -R \\ 0 & R & H\end{pmatrix}</math></center> |
lo que da | lo que da | ||
Revisión de 11:02 13 ene 2021
Contenido |
1 Enunciado
Se tiene un cono homogéneo, de radio de la base R, altura H y masa m distribuida uniformemente.
- Localice la posición del centro de masas del cono empleando un sistema de ejes en el que el cono tiene su vértice en el origen de coordenadas y el eje del cono es el OZ.
- Calcule los momentos de inercia respecto al eje del cono, OZ, y los ejes ortogonales OY y OX
- Halle el momento de inercia respecto a dos ejes, paralelos a OX y OY por el centro de masas.
- Supongamos que el cono se hace girar con velocidad angular constante Ω alrededor de una generatriz, que se toma como eje OZ2.
- ¿Cuánto vale su momento cinético respecto al vértice del cono, O?
- ¿Cuánto vale su energía cinética?
- Calcule la fuerza y el momento que es necesario aplicar en O para mantener el cono en la rotación anterior. ¿Hay algún caso en que se anulen?

2 Centro de masas
Por la simetría del sistema el CM debe estar en x = 0, y = 0, es decir, sobre el eje OZ. La altura a la que se halla el CM la calculamos como
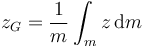
Los elementos de masa los construimos dividiendo el cono en discos horizontales de radio r y espesor diferencial dz
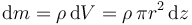
La relación entre el radio de cada disco y su altura lo da el que la generatriz sea una recta
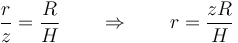
Lo que nos da la integral
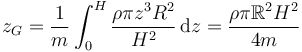
La densidad de masa la relacionamos con la masa a través del volumen que podemos calcular de la misma manera
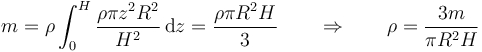
lo que nos da
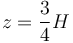
El CM se encuentra a 3/4 de la altura respecto del vértice y 1/4 respecto de la base.
3 Tensor de inercia respecto a O
3.1 Momentos de inercia
3.1.1 Respecto al eje OZ
Este eje es el propio del cono. Como con el centro de masas, descponemos el cono en discos, cada uno de los cuales tiene un momento de inercia
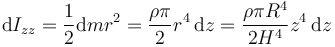
Integramos para todo el cono
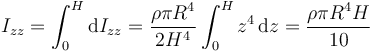
Sustituimos el valor de la densidad de masa y queda
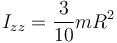
3.1.2 Respecto al eje OX (y al OY)
Por la simetría de revolución del sistema, los momentos de inercia respecto a OX y a OY son iguales.
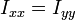
Obtenemos uno de llos descomponiendo de nuevo el cono en discos. Para cada disco, el eje OX es una paralelo a un diámetro del disco. Por el teorema de Steiner, el momento de inercia de cada disco diferencial es
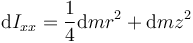
Sustituimos las diferentes cantidades
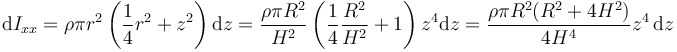
Integramos para todo el cono y queda
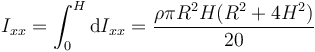
Sustituimos aquí la densidad de masa y obtenemos finalmente
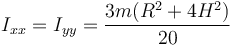
3.2 Productos de inercia
Debido a la simetría del sistema todos los productos de inercia se anulan. En cada una de las integrales por cada valor de x positivo existe uno igual con x negativo y lo mismo con y. Por tanto
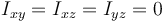
Esto nos deja con un tensor de inercia diagonal
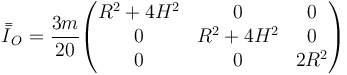
4 Tensor de inercia respecto al CM
El tensor de inercia respecto al CM lo calculamos mediante el teorema de Steiner

Esto nos da
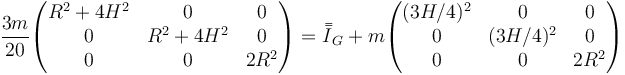
de donde
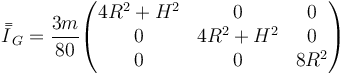
Los momentos de inercia que se piden en el enunciado valen
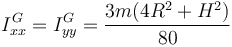
5 Rotación del cono
5.1 Momento cinético
A la hora de calcular el momento cinético tenemos dos caminos:
- expresar la velocidad angular en el sistema ligado al cono y expresar el momento cinético en esta base.
- pasar el tensor de inercia al sistema “2” y calcular el momento cinético en este sistema.
5.1.1 En el sistema ligado
Tomamos un sistema de ejes que en todo momento se hallan respecto al cono como indica la figura, es decir, que si el cono gira, los ejes giran con él. En este sistema el tensor de inercia es siempre el que hemos calculado, es decir, es un tensor diagonal, con
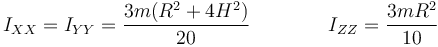
Etiquetaremos como “2” a este sistema.
La velocidad angular, como va a lo largo de una generatriz tendrá la forma
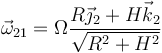
donde hemos elegido como generatriz la que está en el plano OY2Z2 (podíamos haber elegido otra).
Con esto el momento cinético queda
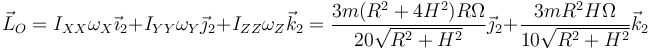
5.1.2 En el sistema intermedio
Consideremos ahora un sistema intermedio “0” en el cual el eje OZ0 es el de rotación pero ahora el cono está girado respecto a los ejes, siendo vertical la generatriz. Este sistema intermedio lo suponemos que también gira con la misma velocidad angular. Solo cambia su orientación respecto al anterior.
El giro que lleva del sistema “0” al “2” es uno de un ángulo β alrededor del eje OX, con
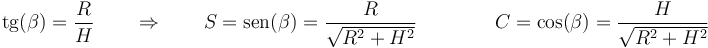
El tensor de inercia en estos nuevos ejes es
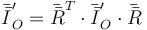
con la matriz de rotación

lo que da
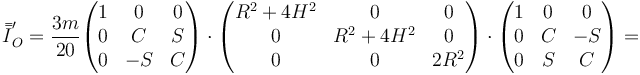
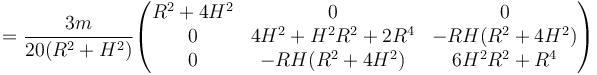
El momento cinético en este sistema de ejes es
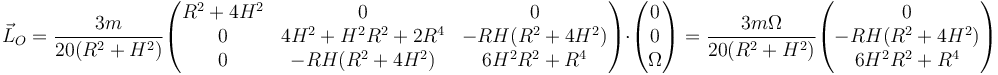
En forma vectorial
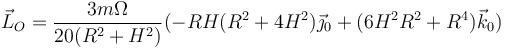
Vemos que es mucho más fácil trabajar en un sistema de ejes principales.





