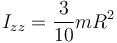Cinética de un cono (CMR)
De Laplace
| Línea 24: | Línea 24: | ||
Lo que nos da la integral | Lo que nos da la integral | ||
| - | <math>z_G=\frac{1}{m}\int_{0}^H \frac{\rho\pi z^3 R^2}{H^2}\,\mathrm{d}z=\frac{\rho\pi \R^2 H^2}{4m}</math> | + | <center><math>z_G=\frac{1}{m}\int_{0}^H \frac{\rho\pi z^3 R^2}{H^2}\,\mathrm{d}z=\frac{\rho\pi \R^2 H^2}{4m}</math></center> |
La densidad de masa la relacionamos con la masa a través del volumen que podemos calcular de la misma manera | La densidad de masa la relacionamos con la masa a través del volumen que podemos calcular de la misma manera | ||
| - | <center><math>m=\rho\int_0^H \frac{\rho\pi z^2 R^2}{H^2}\,\mathrm{d}z = \frac{\rho\pi R^2H}{3}</math></center> | + | <center><math>m=\rho\int_0^H \frac{\rho\pi z^2 R^2}{H^2}\,\mathrm{d}z = \frac{\rho\pi R^2H}{3}\qquad\Rightarrow\qquad \rho=\frac{3m}{\pi R^2 H}</math></center> |
lo que nos da | lo que nos da | ||
| Línea 35: | Línea 35: | ||
El CM se encuentra a 3/4 de la altura respecto del vértice y 1/4 respecto de la base. | El CM se encuentra a 3/4 de la altura respecto del vértice y 1/4 respecto de la base. | ||
| + | |||
| + | ==Tensor de inercia== | ||
| + | ===Momentos de inercia=== | ||
| + | ====Respecto al eje OZ==== | ||
| + | Este eje es el propio del cono. Como con el centro de masas, descponemos el cono en discos, cada uno de los cuales tiene un momento de inercia | ||
| + | |||
| + | <center><math>\matrm{d}I_{zz}= \frac{1}{2}\mathrm{d}m r^2 = \frac{\rho\pi }{2}r^4 \,\mathrm{d}z=\frac{\rho\pi R^4}{2H^4}z^4\,\mathrm{d}z</math></center> | ||
| + | |||
| + | Integramos para todo el cono | ||
| + | |||
| + | <center><math>I_{zz}=\int_0^H\mathrm{d}I_{zz}=\frac{\rho\pi R^4}{2H^4}\int_0^H z^4\,\mathrm{d}z =\frac{\rho\pi R^4H}{10}</math></center> | ||
| + | |||
| + | Sustituimos el valor de la densidad de masa y queda | ||
| + | |||
| + | <center><math>I_{zz}=\frac{3}{10}mR^2</math></center> | ||
| + | ===Productos de inercia=== | ||
Revisión de 19:45 12 ene 2021
Contenido |
1 Enunciado
Se tiene un cono homogéneo, de radio de la base R, altura H y masa m distribuida uniformemente.
- Localice la posición del centro de masas del cono empleando un sistema de ejes en el que el cono tiene su vértice en el origen de coordenadas y el eje del cono es el OZ.
- Calcule los momentos de inercia respecto al eje del cono, OZ, y los ejes ortogonales OY y OX
- Halle el momento de inercia respecto a dos ejes, paralelos a OX y OY por el centro de masas.
- Supongamos que el cono se hace girar con velocidad angular constante Ω alrededor de una generatriz, que se toma como eje OZ2.
- ¿Cuánto vale su momento cinético respecto al vértice del cono, O?
- ¿Cuánto vale su energía cinética?
- Calcule la fuerza y el momento que es necesario aplicar en O para mantener el cono en la rotación anterior. ¿Hay algún caso en que se anulen?

2 Centro de masas
Por la simetría del sistema el CM debe estar en x = 0, y = 0, es decir, sobre el eje OZ. La altura a la que se halla el CM la calculamos como
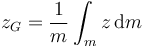
Los elementos de masa los construimos dividiendo el cono en discos horizontales de radio r y espesor diferencial dz
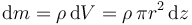
La relación entre el radio de cada disco y su altura lo da el que la generatriz sea una recta
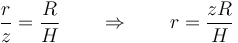
Lo que nos da la integral
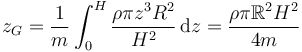
La densidad de masa la relacionamos con la masa a través del volumen que podemos calcular de la misma manera
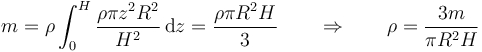
lo que nos da
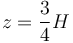
El CM se encuentra a 3/4 de la altura respecto del vértice y 1/4 respecto de la base.
3 Tensor de inercia
3.1 Momentos de inercia
3.1.1 Respecto al eje OZ
Este eje es el propio del cono. Como con el centro de masas, descponemos el cono en discos, cada uno de los cuales tiene un momento de inercia
Integramos para todo el cono
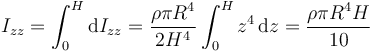
Sustituimos el valor de la densidad de masa y queda