Cinética de un cono (CMR)

(Diferencias entre revisiones)

Revisión de 09:36 12 ene 2021

Se tiene un cono homogéneo, de radio de la base R, altura H y masa m distribuida uniformemente.

Localice la posición del centro de masas del cono empleando un sistema de ejes en el que el cono tiene su vértice en el origen de coordenadas y el eje del cono es el OZ.
Calcule los momentos de inercia respecto al eje del cono, OZ, y los ejes ortogonales OY y OX
Halle el momento de inercia respecto a dos ejes, paralelos a OX y OY por el centro de masas.
Supongamos que el cono se hace girar con velocidad angular constante Ω alrededor de una generatriz, que se toma como eje OZ₂.
1. ¿Cuánto vale su momento cinético respecto al vértice del cono, O?
2. ¿Cuánto vale su energía cinética?
3. Calcule la fuerza y el momento que es necesario aplicar en O para mantener el cono en la rotación anterior. ¿Hay algún caso en que se anulen?

Por la simetría del sistema el CM debe estar en $x = 0$ , $y = 0$ , es decir, sobre el eje OZ. La altura a la que se halla el CM la calculamos como

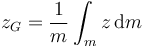
$z_G=\frac{1}{m}\int_{m} z\,\mathrm{d}m$

Los elementos de masa los construimos dividiendo el cono en discos horizontales de radio r y espesor diferencial dz

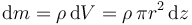
$\mathrm{d}m=\rho\,\mathrm{d}V=\rho\,\pi r^2 \,\mathrm{d}z$

La relación entre el radio de cada disco y su altura lo da el que la generatriz sea una recta

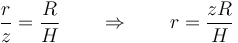
$\frac{r}{z}= \frac{R}{H}\qquad\Rightarrow\qquad r = \frac{zR}{H}$

Lo que nos da la integral

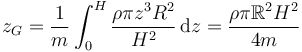
$z_G=\frac{1}{m}\int_{0}^H \frac{\rho\pi z^3 R^2}{H^2}\,\mathrm{d}z=\frac{\rho\pi \R^2 H^2}{4m}$

La densidad de masa la relacionamos con la masa a través del volumen que podemos calcular de la misma manera

$m=\rho\int_0^H \frac{\rho\pi z^2 R^2}{H^2}\,\mathrm{d}z = \frac{\rho\pi R^2H}{3}$

lo que nos da

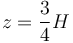
$z = \frac{3}{4}H$

El CM se encuentra a 3/4 de la altura respecto del vértice y 1/4 respecto de la base.

@@ Línea 9: / Línea 9: @@
 ## Calcule la fuerza y el momento que es necesario aplicar en O para mantener el cono en la rotación anterior. ¿Hay algún caso en que se anulen?
 <center>[[Archivo:cono-solido-ejes.png|200px]]</center>
+==Centro de masas==
+Por la simetría del sistema el CM debe estar en <math>x=0</math>, <math>y = 0</math>, es decir, sobre el eje OZ. La altura a la que se halla el CM la calculamos como
+<math>z_G=\frac{1}{m}\int_{m} z\,\mathrm{d}m</math>
+Los elementos de masa los construimos dividiendo el cono en discos horizontales de radio r y espesor diferencial dz
+<center><math>\mathrm{d}m=\rho\,\mathrm{d}V=\rho\,\pi r^2 \,\mathrm{d}z</math></center>
+La relación entre el radio de cada disco y su altura lo da el que la generatriz sea una recta
+<center><math>\frac{r}{z}= \frac{R}{H}\qquad\Rightarrow\qquad r = \frac{zR}{H}</math></center>
+Lo que nos da la integral
+<math>z_G=\frac{1}{m}\int_{0}^H \frac{\rho\pi z^3 R^2}{H^2}\,\mathrm{d}z=\frac{\rho\pi \R^2 H^2}{4m}</math>
+La densidad de masa la relacionamos con la masa a través del volumen que podemos calcular de la misma manera
+<center><math>m=\rho\int_0^H \frac{\rho\pi z^2 R^2}{H^2}\,\mathrm{d}z = \frac{\rho\pi R^2H}{3}</math></center>
+lo que nos da
+<center><math>z = \frac{3}{4}H</math></center>
+El CM se encuentra a 3/4 de la altura respecto del vértice y 1/4 respecto de la base.