Entrar Página Discusión Historial Go to the site toolbox

Dinámica de masa en varilla articulada (CMR)

De Laplace

(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Se tiene un sistema horizontal en el que una partícula P, de masa m, se encuentra unida a una varilla de longitud <math>\ell</math> cuyo otro extremo, A, se halla…')
Edición más nueva →

Revisión de 13:35 9 ene 2021

1 Enunciado

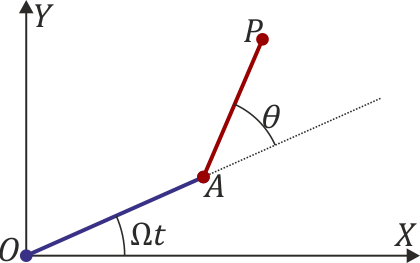
Se tiene un sistema horizontal en el que una partícula P, de masa m, se encuentra unida a una varilla de longitud 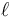\ell cuyo otro extremo, A, se halla articulado a una segunda varilla, de longitud b, cuyo segundo extremo, O, está fijo. La varilla OA gira en torno a O con velocidad angular constante Ω, mientras que la varilla AP puede girar libremente en torno a A. Sea θ el ángulo que AP forma con la prolongación de OA.

Archivo:masa-varilla-articulada.png
  1. ¿Qué vínculo hay entre las coordenadas cartesianas de P? Escríbalo en forma geométrica, cinemática y pfaffiana.
  2. Obtenga la ecuación de movimiento para el ángulo θ.
  3. ¿Qué puntos de equilibrio hay para el ángulo θ? ¿Son estables o inestables?

2 Ecuación de vínculo

La ecuación de vínculo sobre P es que su distancia al punto A es constante

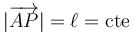
|\overrightarrow{AP}|=\ell=\mathrm{cte}

Se trata de escribir esta relación en términos de las coordenadas cartesianas de P.

La posición de A es en todo momento

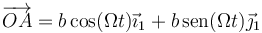
\overrightarrow{OA}=b\cos(\Omega t)\vec{\imath}_1+b\,\mathrm{sen}(\Omega t)\vec{\jmath}_1

con lo que la ecuación de vínculo se puede escribir en la forma

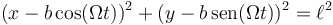
(x-b\cos(\Omega t))^2+(y-b\,\mathrm{sen}(\Omega t))^2 = \ell^2

Esta sería la forma geométrica.

Obtenemos la forma cinemática derivando esta respecto al tiempo.

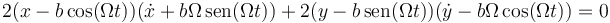
2(x-b\cos(\Omega t))(\dot{x}+b\Omega\,\mathrm{sen}(\Omega t))+2(y-b\,\mathrm{sen}(\Omega t))(\dot{y}-b\Omega\cos(\Omega t))=0

Simplificando por 2 y agrupando términos queda

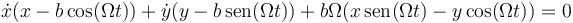
\dot{x}(x-b\cos(\Omega t))+\dot{y}(y-b\,\mathrm{sen}(\Omega t))+b\Omega(x\,\mathrm{sen}(\Omega t)-y\cos(\Omega t))=0

La forma pfaffiana se obteien multiplicando la condición cinemática por dt

\mathrm{d}x(x-b\cos(\Omega t))+\mathrm{d}y(y-b\,\mathrm{sen}(\Omega t))+b\Omega\,\mathrm{d}t(x\,\mathrm{sen}(\Omega t)-y\cos(\Omega t))=0
Obtenido de "http://tesla.us.es/wiki/index.php/Din%C3%A1mica_de_masa_en_varilla_articulada_(CMR)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace