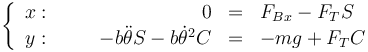Varilla apoyada en una esquina (CMR)
De Laplace
| Línea 18: | Línea 18: | ||
Separando por componentes | Separando por componentes | ||
| - | <center><math>\left\{\begin{array}{rcrcl}x:&\ | + | <center><math>\left\{\begin{array}{rcrcl}x:&\quad&0&=&F_{Ax}+F_TS\\y: &\quad&0&=&-mg+F_{Ay}-F_TC\end{array}\right.</math></center> |
Para la masa B, actúan su peso, la reacción normal de la pared y la tensión. No hay rozamiento | Para la masa B, actúan su peso, la reacción normal de la pared y la tensión. No hay rozamiento | ||
| Línea 27: | Línea 27: | ||
Separando por componentes | Separando por componentes | ||
| - | <center><math>\left\{\begin{array}{rcrcl}x:&\ | + | <center><math>\left\{\begin{array}{rcrcl}x:&\quad&0&=&F_{Bx}-F_TS\\y: &\quad&0&=&-mg+F_TC\end{array}\right.</math></center> |
De aquí obtenemos la tensión | De aquí obtenemos la tensión | ||
| Línea 54: | Línea 54: | ||
==Estado de movimiento== | ==Estado de movimiento== | ||
| - | == | + | Si no hay rozamiento, la barra desliza apoyada en la pared y en el suelo. La masa A se mueve horizontalmente con posición, velocidad y aceleración |
| + | |||
| + | <center><math>\overrightarrow{OA}=bS\vec{\imath}\qquad\qquad \vec{v}_A=b\dot{\theta}C\vec{\imath}\qquad \vec{a}_A = b\ddot{\theta}C-b\dot{\theta}^2S\vec{\imath}</math></center> | ||
| + | |||
| + | y las de la masa B son | ||
| + | |||
| + | <center><math>\overrightarrow{OB}=bC\vec{\jmath}\qquad\qquad \vec{v}_B=-b\dot{\theta}S\vec{\imath}\qquad \vec{a}_B = -b\ddot{\theta}S-b\dot{\theta}^2C\vec{\imath}</math></center> | ||
| + | |||
| + | Por ello, las ecuaciones de movimiento para la masa A quedan | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcrcl}x:&\quad&b\ddot{\theta}C-b\dot{\theta}^2S&=&F_TS\\y: &\quad&0&=&-mg+F_{Ay}-F_TC\end{array}\right.</math></center> | ||
| + | |||
| + | y las de la masa B | ||
| + | |||
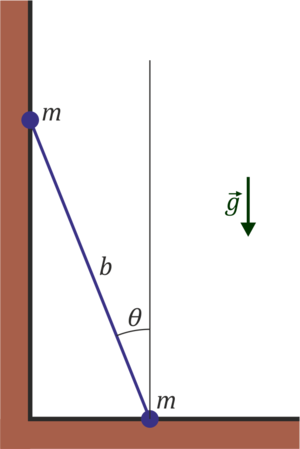
| + | <center><math>\left\{\begin{array}{rcrcl}x:&\quad&0&=&F_{Bx}-F_TS\\y: &\quad&-b\ddot{\theta}S-b\dot{\theta}^2C&=&-mg+F_TC\end{array}\right.</math></center> | ||
==Separación de la pared== | ==Separación de la pared== | ||
Revisión de 20:06 3 ene 2021
Contenido |
1 Enunciado
Dos masas iguales m están unidas por una varilla rígida ideal de longitud b. La varilla está apoyada en el suelo y en una pared vertical, formando la varilla un ángulo θ con la vertical. Todo el sistema está contenido en el plano vertical OXY
- Suponga que el sistema está en equilibrio. Calcule el mínimo valor que debe tener el coeficiente de rozamiento μ entre la varilla y el suelo para que esto ocurra. Para esta situación, ¿cuánto valen las reacciones normales del suelo y la pared, la fuerza de rozamiento y la tensión de la varilla?
- Suponga que no existe rozamiento y que la varilla va cayendo apoyada en el suelo y la pared. Para el momento en que la varilla forma un ángulo θ con la vertical y este ángulo varía con una velocidad
 , ¿cuánto valen las reacciones y la tensión?
, ¿cuánto valen las reacciones y la tensión?
- Determine la ecuación de movimiento para la varilla.
- Si inicialmente la varilla se encuentra en reposo en posición vertical y a partir de ahí comienza a deslizar, ¿para qué ángulo se separa de la pared?
2 Estado de equilibrio
Si las masas permanecen reposo, la suma de fuerzas sobre cada una de ellas dee ser nula. Sobre la partícula A, situada en el suelo, actúan su peso, la rección normal del suelo, la fuerza de rozamiento, horizontal, y la tensión de la varilla. La condición de equilibrio es
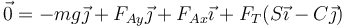
Separando por componentes
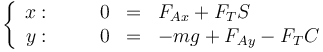
Para la masa B, actúan su peso, la reacción normal de la pared y la tensión. No hay rozamiento
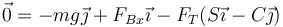
Separando por componentes
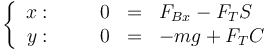
De aquí obtenemos la tensión
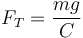
La reacción en B
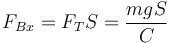
La fuerza normal en A
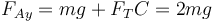
y la fuerza de rozamiento
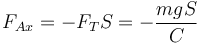
El valor mínimo del coeficiente de rozamiento lo obtenemos de la condición

que en este caso nos da
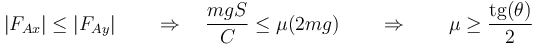
3 Estado de movimiento
Si no hay rozamiento, la barra desliza apoyada en la pared y en el suelo. La masa A se mueve horizontalmente con posición, velocidad y aceleración
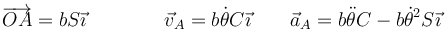
y las de la masa B son
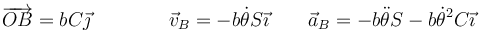
Por ello, las ecuaciones de movimiento para la masa A quedan
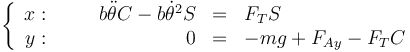
y las de la masa B