Mono intentado alcanzar unos plátanos
De Laplace
(→Polea con masa) |
|||
| Línea 9: | Línea 9: | ||
== Polea sin masa == | == Polea sin masa == | ||
[[Archivo:F1GIC-mono-platanos-poleasinmasa.png|right]] | [[Archivo:F1GIC-mono-platanos-poleasinmasa.png|right]] | ||
| - | Consideramos que el mono y el racimo de plátanos forman un sistema de dos partículas. El sistema se puede modelar con la figura de la derecha, con las masas <math>m</math> (el mono) y <math>p</math> (los plátanos), ambos de la misma magnitud | + | Consideramos que el mono y el racimo de plátanos forman un sistema de dos partículas. El sistema se puede modelar con la figura de la derecha, con las masas <math>m</math> (el mono) y <math>p</math> (los plátanos), ambos de la misma magnitud <math>m_0</math>. Hay que señalar que el mono sube por la cuerda. Por tanto, tanto <math>\vec{v}_m</math> como <math>\vec{v}_p</math> están dirigidas hacia arriba. |
| + | <center> | ||
| + | <math> | ||
| + | \vec{v}_m = -v_m\,\vec{\imath}, \qquad \vec{v}_p = -v_p\,\vec{\imath}. | ||
| + | </math> | ||
| + | </center> | ||
| + | Ponemos el signo negativo en las componentes para que <math>v_m</math> y <math>v_p</math> sean positivos. | ||
| + | |||
| + | El momento angular de este sistema respecto al centro de la polea es | ||
<center> | <center> | ||
<math> | <math> | ||
| Línea 19: | Línea 27: | ||
<math> | <math> | ||
\begin{array}{ll} | \begin{array}{ll} | ||
| - | \vec{L}_O^m & = \vec{r}_m\times(m_o\vec{v}_m) = m_0R | + | \vec{L}_O^m & = \vec{r}_m\times(m_o\vec{v}_m) = -m_0R v_m\,\vec{k}\\ |
& \vec{r}_m = x_m\,\vec{\imath} - R\,\vec{\jmath}\\ | & \vec{r}_m = x_m\,\vec{\imath} - R\,\vec{\jmath}\\ | ||
| - | & \vec{v}_m = | + | & \vec{v}_m = -v_m\,\vec{\imath} |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Línea 29: | Línea 37: | ||
<math> | <math> | ||
\begin{array}{ll} | \begin{array}{ll} | ||
| - | \vec{L}_O^p & = \vec{r}_p\times(m_o\vec{v}_p) = | + | \vec{L}_O^p & = \vec{r}_p\times(m_o\vec{v}_p) = m_0R v_p\,\vec{k}\\ |
& \vec{r}_p = x_p\,\vec{\imath} + R\,\vec{\jmath}\\ | & \vec{r}_p = x_p\,\vec{\imath} + R\,\vec{\jmath}\\ | ||
| - | & \vec{v}_p = | + | & \vec{v}_p = -v_p\,\vec{\imath} |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Línea 38: | Línea 46: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \vec{L} = m_0R\,( | + | \vec{L} = m_0R\,(v_p - v_m)\,\vec{k} |
</math> | </math> | ||
</center> | </center> | ||
| - | Como se observa en el dibujo, las únicas fuerzas externas que actúan sobre el sistema de dos partículas son sus pesos. | + | Como se observa en el dibujo, las únicas fuerzas externas que actúan sobre el sistema de dos partículas son sus pesos y la fuerza vincular, <math>\vec{O}</math>, que actúa sobre el centro de la polea para que esta no se caiga. <center> |
| - | <center> | + | |
<math> | <math> | ||
| - | \vec{P}_m = m_0g\,\vec{\imath}, \qquad \vec{P}_p = m_0g\,\vec{\imath} | + | \vec{P}_m = m_0g\,\vec{\imath}, \qquad \vec{P}_p = m_0g\,\vec{\imath}, \qquad \vec{O} = O_x\,\vec{\imath} + O_y\,\vec{\jmath}. |
</math> | </math> | ||
</center> | </center> | ||
| - | Las fuerzas | + | Las fuerzas entre el mono y los plátanos y la cuerda no cuentan en la evolución del momento angular total pues son fuerzas internas. La fuerza <math>\vec{O}</math> no crea momento respecto al punto <math>O</math> porque está aplicada en el. Aplicando el T.M.C. en el punto <math>O</math> tenemos |
<center> | <center> | ||
<math> | <math> | ||
| Línea 60: | Línea 67: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \vec{L}_O = m_0R( | + | \vec{L}_O = m_0R(v_p - v_m)\,\vec{k}=\vec{0} |
\Longrightarrow | \Longrightarrow | ||
| - | + | v_p = v_m | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 85: | Línea 92: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | Aquí, <math>I</math> es el momento de inercia del aro respecto a un eje perpendicular a él que pasa por su centro. El vector <math>\vec{\omega}</math> describe la rotación de la polea. Como se ve en el dibujo, El punto <math>A</math> de la cuerda tiene la misma velocidad que | + | Aquí, <math>I</math> es el momento de inercia del aro respecto a un eje perpendicular a él que pasa por su centro. El vector <math>\vec{\omega}</math> describe la rotación de la polea. Como se ve en el dibujo, El punto <math>A</math> de la cuerda tiene la misma velocidad que los plátanos. Pero el punto <math>B</math> de la polea también tiene la misma velocidad. Entonces tenemos |
<center> | <center> | ||
<math> | <math> | ||
| Línea 94: | Línea 101: | ||
& \overrightarrow{OB} = R\,\vec{\jmath}. | & \overrightarrow{OB} = R\,\vec{\jmath}. | ||
\end{array}\\ | \end{array}\\ | ||
| - | \vec{v}_B = \vec{v}_p = | + | \vec{v}_B = \vec{v}_p = -v_p\,\vec{\imath} |
\end{array} | \end{array} | ||
\right| | \right| | ||
\to | \to | ||
| - | \omega = | + | \omega = v_p/R. |
</math> | </math> | ||
</center> | </center> | ||
| Línea 104: | Línea 111: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \vec{L}_O = R\,((m_0+M) | + | \vec{L}_O = R\,((m_0+M)v_p - m_0v_m)\,\vec{k}. |
</math> | </math> | ||
</center> | </center> | ||
| - | La figura muestra | + | La figura muestra la fuerza exterior que hay que añadir cuando la polea tiene masa: su peso <math>\vec{P}_a</math>. |
| - | Ahora bien, estas | + | Ahora bien, estas nueva fuerza, al igual que la fuerza vincular <math>O</math>, se aplica en el punto <math>O</math>, por lo que no contribuye al momento total de fuerzas externas respecto a <math>O</math>. Por tanto, se cumple otra vez |
<center> | <center> | ||
<math> | <math> | ||
| Línea 120: | Línea 127: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | (m_0+M) | + | (m_0+M)v_p - m_0v_m = 0 \to |
| - | + | v_p = \dfrac{m_0}{m_0+M}\,v_m | |
</math> | </math> | ||
</center> | </center> | ||
| - | El enunciado dice que, en este caso, <math> | + | El enunciado dice que, en este caso, <math>v_m = v_0</math>. Entonces |
<center> | <center> | ||
<math> | <math> | ||
| - | \vec{v}_m = | + | \vec{v}_m = v_0\,\vec{\imath}, \qquad \vec{v}_p = \dfrac{m_0}{m_0+M}\,v_0\,\vec{\imath}. |
</math> | </math> | ||
</center> | </center> | ||
Revisión de 17:58 23 dic 2020
Contenido |
1 Enunciado
Un mono de masa m0 cuelga de una cuerda ideal inextensible y sin masa, que está enrollada en una polea de radio R. En el otro extremo de la cuerda hay un racimo de plátanos que tienen la misma masa m0 del mono. Los plátanos están por encima del mono, como se indica en la figura. Éste los ve y comienza a trepar por la cuerda para intentar alcanzarlos.
- Supongamos que la masa de la polea es despreciable. ¿Consigue el mono atrapar los platanos antes de que estos alcancen la altura de la polea?
- Supongamos ahora que la polea es un aro con masa M. En el instante inicial los plátanos están a una distancia L de la altura de la polea y el mono a una distancia 2L. El mono sube la cuerda con velocidad v0 respecto a la polea. ¿Que condición debe cumplir M para que el mono pueda alcanzar los plátanos antes de que estos lleguen a la polea?
2 Solución
2.1 Polea sin masa
Consideramos que el mono y el racimo de plátanos forman un sistema de dos partículas. El sistema se puede modelar con la figura de la derecha, con las masas m (el mono) y p (los plátanos), ambos de la misma magnitud m0. Hay que señalar que el mono sube por la cuerda. Por tanto, tanto 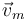 como
como 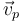 están dirigidas hacia arriba.
están dirigidas hacia arriba.

Ponemos el signo negativo en las componentes para que vm y vp sean positivos.
El momento angular de este sistema respecto al centro de la polea es
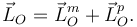
El momento angular del mono es

El momento angular del racimo de plátanos es
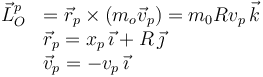
Por tanto, el momento angular total es
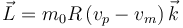
 , que actúa sobre el centro de la polea para que esta no se caiga.
, que actúa sobre el centro de la polea para que esta no se caiga. 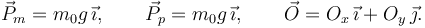
Las fuerzas entre el mono y los plátanos y la cuerda no cuentan en la evolución del momento angular total pues son fuerzas internas. La fuerza 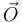 no crea momento respecto al punto O porque está aplicada en el. Aplicando el T.M.C. en el punto O tenemos
no crea momento respecto al punto O porque está aplicada en el. Aplicando el T.M.C. en el punto O tenemos
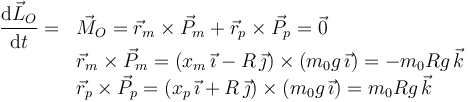
Es decir,  es constante durante todo el proceso. Pero en el instante inicial era nulo, pues tanto el mono como los plátanos estaban en reposo. Entonces es nulo en todo instante y por tanto
es constante durante todo el proceso. Pero en el instante inicial era nulo, pues tanto el mono como los plátanos estaban en reposo. Entonces es nulo en todo instante y por tanto
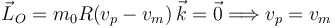
El mono y los plátanos suben con la misma velocidad. Por tanto el mono no alcanza los plátanos antes de que éstos lleguen a la polea.
2.2 Polea con masa
Ahora tenemos que considerar un sistema formado por el mono, los plátanos y el aro. El momento angular total en O es
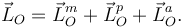
Las expresiones para los momentos del mono y los plátanos son iguales que antes. Para el aro tenemos
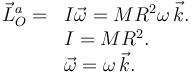
Aquí, I es el momento de inercia del aro respecto a un eje perpendicular a él que pasa por su centro. El vector  describe la rotación de la polea. Como se ve en el dibujo, El punto A de la cuerda tiene la misma velocidad que los plátanos. Pero el punto B de la polea también tiene la misma velocidad. Entonces tenemos
describe la rotación de la polea. Como se ve en el dibujo, El punto A de la cuerda tiene la misma velocidad que los plátanos. Pero el punto B de la polea también tiene la misma velocidad. Entonces tenemos
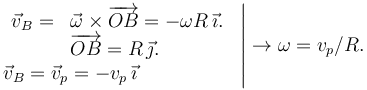
Con esto, el momento angular total respecto al punto O es
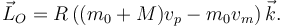
La figura muestra la fuerza exterior que hay que añadir cuando la polea tiene masa: su peso  .
.
Ahora bien, estas nueva fuerza, al igual que la fuerza vincular O, se aplica en el punto O, por lo que no contribuye al momento total de fuerzas externas respecto a O. Por tanto, se cumple otra vez

Y, entonces

El enunciado dice que, en este caso, vm = v0. Entonces
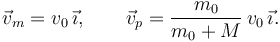
Tanto el mono como los plátanos realizan movimientos rectilíneos uniformes. El enunciado nos dice que las condiciones iniciales son

Utilizando las expresiones del movimiento rectilíneo uniforme tenemos
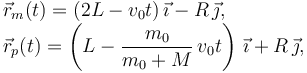
Cuando los plátanos y el mono están a la misma altura las componentes en X deben ser iguales. Así averiguamos el instante t0 para el que ocurre
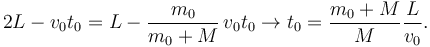
Para que el mono alcance los plátanos antes de que estos lleguen a la polea el valor de xm en el instante t0 debe ser mayor que cero
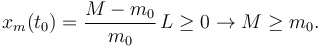
Es decir, para que el mono alcance los plátanos la masa de la polea debe ser mayor que la del mono. Si son iguales el mono y los plátanos llegan a la altura del centro del aro a la vez.








