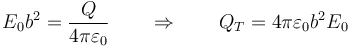Campo eléctrico central (GIOI)
De Laplace
(Diferencias entre revisiones)
| Línea 12: | Línea 12: | ||
Para conocer la carga total poremos aplicar la ley de Gauss | Para conocer la carga total poremos aplicar la ley de Gauss | ||
| - | <math>Q_\mathrm{int}=\varepsilon_0\oint \vec{E}\cdot\mathrm{d}\vec{S}</math> | + | <center><math>Q_\mathrm{int}=\varepsilon_0\oint \vec{E}\cdot\mathrm{d}\vec{S}</math></center> |
Puesto que queremos hallar la carga total, la superficie de integración debe ser una que contenga toda la carga. Esta superficie es una esfera cuyo radio tiende a infinito. Por tanto | Puesto que queremos hallar la carga total, la superficie de integración debe ser una que contenga toda la carga. Esta superficie es una esfera cuyo radio tiende a infinito. Por tanto | ||
| Línea 24: | Línea 24: | ||
Puesto que el integrando tiene el mismo valor en todos los puntos de la superficie | Puesto que el integrando tiene el mismo valor en todos los puntos de la superficie | ||
| - | <center><math>\oint_{r=R} \vec{E}\cdot\matrm{d}\vec{S}=\oint_{r=R} E(r)\,\ | + | <center><math>\oint_{r=R} \vec{E}\cdot\matrm{d}\vec{S}=\oint_{r=R} E(r)\,\mathrm{d}S=E(R)S=4\pi R^2 E(R)</math></center> |
y por tanto la carga total es | y por tanto la carga total es | ||
| - | <center><math>Q_T=\lim_{R\to infty}\varepsilon_0(4\pi R^2)E_0\left(\frac{b}{R}\right)^2=4\ | + | <center><math>Q_T=\lim_{R\to infty}\varepsilon_0(4\pi R^2)E_0\left(\frac{b}{R}\right)^2=4\pi\varepsilon_0 b^2 E_0</math></center> |
===Identificando el campo=== | ===Identificando el campo=== | ||
| + | Podemos llegar directamente a este resultado observando que para r > b el campo es de la forma | ||
| + | |||
| + | <center><math>\vec{E}=\frac{R_0b^2}{r^2}\vec{u}_r</math></center> | ||
| + | |||
| + | es decir: | ||
| + | |||
| + | * es radial | ||
| + | * depende solo de la distancia al origen | ||
| + | * va como la inversa del cuadrado de la distancia al origen | ||
| + | |||
| + | Estas propiedades lo identifican como el campo de una carga puntual | ||
| + | |||
| + | <center><math>\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{r^2}\vec{u}_r</math></center> | ||
| + | |||
| + | Igualando los coeficientes | ||
| + | |||
| + | <center><math>E_0 b^2 = \frac{Q}{4\pi\varepsilon_0}\qquad\Rightarrow\qquad Q_T=4\pi\varepsilon_0 b^2 E_0</math></center> | ||
==Densidad de carga== | ==Densidad de carga== | ||
==Potencial eléctrico en el origen== | ==Potencial eléctrico en el origen== | ||
Revisión de 19:29 8 mar 2020
Contenido |
1 Enunciado
El campo eléctrico en todos los puntos del espacio viene dado por la expresión
-
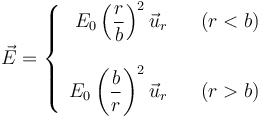
¿Cuánto vale la carga total almacenada en el sistema?
-
¿Cuánto vale la densidad de carga ρ = ρ(r)?
-
¿Cuánto vale el potencial eléctrico en el origen de coordenadas (tomando como origen de potencial el infinito)?
- ¿Cuánta energía almacena este sistema?
2 Carga total
2.1 A partir del flujo
Para conocer la carga total poremos aplicar la ley de Gauss
Puesto que queremos hallar la carga total, la superficie de integración debe ser una que contenga toda la carga. Esta superficie es una esfera cuyo radio tiende a infinito. Por tanto
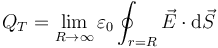
Sobre una superficie esférica de gran radio
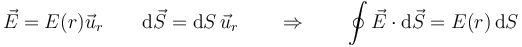
Puesto que el integrando tiene el mismo valor en todos los puntos de la superficie
y por tanto la carga total es
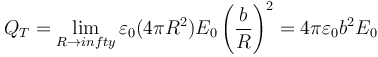
2.2 Identificando el campo
Podemos llegar directamente a este resultado observando que para r > b el campo es de la forma
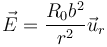
es decir:
- es radial
- depende solo de la distancia al origen
- va como la inversa del cuadrado de la distancia al origen
Estas propiedades lo identifican como el campo de una carga puntual
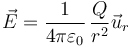
Igualando los coeficientes
