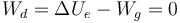Conexión de una fuente a un conductor
De Laplace
(→Variación de le energía) |
|||
| Línea 24: | Línea 24: | ||
Nótese que el conductor no tiene “memoria”, es decir, su carga final es independiente de la que tuviera en un principio. | Nótese que el conductor no tiene “memoria”, es decir, su carga final es independiente de la que tuviera en un principio. | ||
| - | ==Variación de | + | ==Variación de la energía== |
La energía electrostática inicial vale | La energía electrostática inicial vale | ||
última version al 14:43 3 mar 2020
Contenido |
1 Enunciado
Un determinado sistema está formado exclusivamente por un conductor de capacidad C. Inicialmente este conductor almacena una carga QA.
Una fuente de tensión continua VB se conecta al conductor mediante un interruptor que se cierra bruscamente.
- ¿Cuánto cambia la carga almacenada en el conductor?
- ¿Cuánto cambia la energía electrostática del sistema?
- ¿Qué trabajo realiza la fuente en este proceso? ¿En qué caso es nulo?
- ¿Cuánta energía se disipa? ¿En que caso es nula?
- Supóngase ahora que la fuente es una de tensión regulable que se hace variar lentamente desde VA (la correspondiente al estado inicial) a VB. ¿Cómo quedan en ese caso las respuestas a los tres apartados anteriores?
2 Variación de la carga
Inicialmente el conductor almacena una carga Q_A y se halla a un potencial
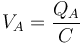
Tras la conexión, su potencial es el que fije la fuente, VB, y su carga vale
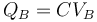
por lo que la variación de la carga del conductor es igual a
Nótese que el conductor no tiene “memoria”, es decir, su carga final es independiente de la que tuviera en un principio.
3 Variación de la energía
La energía electrostática inicial vale
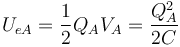
y la final
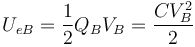
siendo el incremento
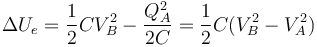
Este incremento puede ser tanto positivo como negativo, dependiendo de si el potencial final es mayor o menor que el inicial.
4 Trabajo y energía disipada
Un generador de continua mantiene fijado el potencial a base de añadir o quitar carga del conductor. El trabajo para mover una carga q desde tierra (potencial 0) al potencial VB es el producto de la carga por el potencial qVB. Para mover una carga ΔQ realizará un trabajo
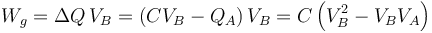
Este trabajo puede ser positivo, negativo o nulo.
Es nulo si:
- VB = VA, es decir, ya el conductor se halla al potencial final, por lo que no hay un trasvase de carga.
- VB = 0, es decir, realmente no hay generador, sino simplemente una conexión a tierra por la que se descarga el conductor.
5 Energía disipada
El trabajo realizado por el generador no coincide con el incremento de la energía electrostática
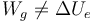
siendo la diferencia la llamada energía disipada
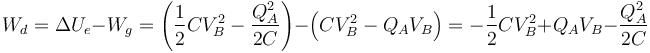
Esta cantidad es siempre negativa o nula, ya que es proporcional al cuadrado de una diferencia
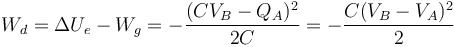
Puesto que
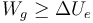
esto quiere decir que parte del trabajo realizado por el generador no se emplea en aumentar la energía electrostática. De acuerdo con las leyes de la termodinámica, pueden ocurrir dos cosas:
- Que escape en forma de calor
- Que se almacene en forma de energía interna, lo que se manifiesta como un incremento de la temperatura del conductor.
Esta producción de calor o incremento de temperatura se da tanto cuando el trabajo es positivo como cuando es negativo. Solo se anula cuando el trabajo y la variación de la energía electrostática son también nulos.
6 Caso cuasiestático
Cuando el potencial varía gradualmente de su valor inicial al final no cambia ni el incremento de la carga
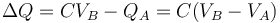
ni el de la energía electrostática
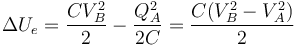
ya que al tratarse de funciones de estado solo dependen del punto de partida y del de llegada.
No ocurre lo mismo con el trabajo del generador, que sí depende del proceso. Si el potencial varía gradualmente quiere decir que la carga que va colocando el generador se sitúa cada vez a un potencial diferente, por lo que habrá que descomponer el proceso en pequeños pasos, en los cuales el generador realiza un trabajo diferencial
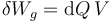
Cuando el potencial del conductor pasa de V a V+dV, la carga almacenada en él pasa de CV a C(V+dV), por lo que el incremento diferencial de carga vale
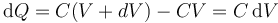
y el trabajo diferencial es
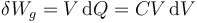
Para hallar el trabajo total sumamos todos los pasos diferenciales, es decir, integramos,
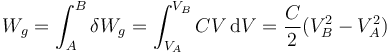
Vemos que ahora sí que coincide el trabajo del generador con el incremento de energía electrostática
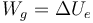
y por tanto en este proceso cuasiestático no se disipa energía