Problemas de electrostática en medios materiales (GIOI)
De Laplace
(→Esfera conductora en equilibrio electrostático (II)) |
(→Dos esferas conductoras concéntricas) |
||
| Línea 39: | Línea 39: | ||
[[Dos esferas conductoras concéntricas|Solución]] | [[Dos esferas conductoras concéntricas|Solución]] | ||
| + | |||
| + | ==Conexión de dos esferas alejadas== | ||
| + | {{nivel|2}} Se tiene un conductor formado por dos esferas de radios <math>a</math> y <math>b</math> (<math>a<b</math>), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga <math>Q_0</math>. | ||
| + | |||
| + | # ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada? | ||
| + | # ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie? | ||
| + | |||
| + | <center>[[Imagen:dosesferashilo-02.png]]</center> | ||
| + | |||
| + | [[Conexión de dos esferas alejadas|Solución]] | ||
Revisión de 14:38 3 mar 2020
Contenido |
1 Acumulación de carga en un conductor
Sobre una lámina metálica de cobre, de 1m² de área y 1cm de espesor se aplica perpendicularmente un campo eléctrico de 1V/m de intensidad. Calcule cuantos electrones se acumulan en la cara del conductor cargada negativamente. ¿Qué proporción suponen estos electrones respecto al total de electrones disponibles, que en el caso del cobre, es 1 por átomo?
2 Esfera conductora en equilibrio electrostático
![]() Se tiene una esfera metálica maciza de radio a y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Q calcule:
Se tiene una esfera metálica maciza de radio a y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Q calcule:
- el potencial y el campo eléctrico en todos los puntos del espacio.
- el voltaje al que se encuentra
- la densidad superficial de carga.
- la energía electrostática que almacena.
- Particularice los resultados anteriores para un radio
 y una carga
y una carga 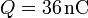 .
.
3 Esfera conductora en equilibrio electrostático (II)
![]() Suponga ahora que lo que se conoce inicialmente su voltaje V0, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje
Suponga ahora que lo que se conoce inicialmente su voltaje V0, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje 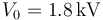 .
.
4 Dos esferas conductoras concéntricas
![]() Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 9 mm. El “2” es una corona esférica gruesa, concéntrica con la anterior, de radio interior 12 mm y exterior 18 mm. Halle la carga almacenada y el potencial al que se encuentra cada conductor, así como
la energía almacenada en el sistema, para los siguientes casos:
Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 9 mm. El “2” es una corona esférica gruesa, concéntrica con la anterior, de radio interior 12 mm y exterior 18 mm. Halle la carga almacenada y el potencial al que se encuentra cada conductor, así como
la energía almacenada en el sistema, para los siguientes casos:
- La esfera almacena una carga de +4 nC y la corona está aislada y descargada.
- La esfera está aislada y descargada y la corona almacena +6 nC
- La esfera almacena una carga de +4 nC y la corona de +6 nC
- La esfera almacena una carga de −4 nC y la corona de +4 nC
- La esfera almacena una carga de −4 nC y la corona de +6 nC
- La esfera almacena una carga de +4 nC y la corona está a tierra
- La esfera está a tierra y la corona almacena una carga de +6 nC
- La esfera está a +2 kV y la corona está a tierra.
- La esfera está a tierra y la corona a +2 kV.
- La esfera y la corona están a +2 kV
- La esfera está a +2 kV y la corona está a −2 kV.
Sugerencia: Resuélvase primero el caso general, estableciendo relaciones entre las cargas y los potenciales, y expresiones para la energía. Puede ser útil construir un circuito equivalente.
5 Conexión de dos esferas alejadas
![]() Se tiene un conductor formado por dos esferas de radios a y b (a < b), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga Q0.
Se tiene un conductor formado por dos esferas de radios a y b (a < b), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga Q0.
- ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada?
- ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie?






