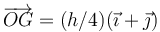Centro de masas de una L
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Se tiene un sólido en forma de L con los brazos de igual longitud <math>h</math>, siendo <math>M</math> la masa total del sólido, distribuida uniformemente. <ce…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se tiene un sólido en forma de L con los brazos de igual longitud <math>h</math>, siendo <math> | + | Se tiene un sólido en forma de L con los brazos de igual longitud <math>h</math>, siendo <math>m</math> la masa total del sólido, distribuida uniformemente. |
<center> [[Archivo:Inercia-L-01.png]] </center> | <center> [[Archivo:Inercia-L-01.png]] </center> | ||
| Línea 15: | Línea 15: | ||
La intersección de esta recta con la bisectriz en el punto | La intersección de esta recta con la bisectriz en el punto | ||
| - | <center><math>\ | + | <center><math>\overrightarrow{OG}=(h/4)(\vec{\imath}+\vec{\jmath})</math></center> |
última version al 11:17 1 ene 2006
1 Enunciado
Se tiene un sólido en forma de L con los brazos de igual longitud h, siendo m la masa total del sólido, distribuida uniformemente.
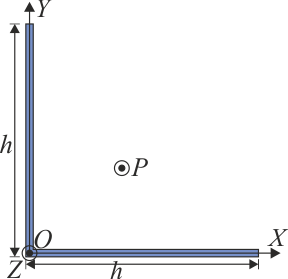
Considerando un sistema de ejes con origen en el vértice y ejes OX y OY paralelos a los brazos de la L, ¿dónde se encuentra en centro de masas del sólido?
2 Solución
or la simetría del sistema, el CM debe hallarse sobre la bisectriz de la escuadra.
Además, debe encontrarse en la línea que une los centros de masas de cada uno de los brazos. Estos centros de masas están en los centros respectivos, por lo que el CM de la figura se halla en la recta que va de 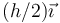 a
a  .
.
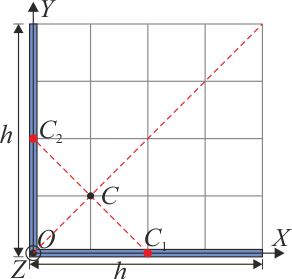
La intersección de esta recta con la bisectriz en el punto