Máquina de Atwood con resorte
De Laplace
| Línea 77: | Línea 77: | ||
<center><math>A=15\,\mathrm{cm}-13\,\mathrm{cm}=2\,\mathrm{cm}</math></center> | <center><math>A=15\,\mathrm{cm}-13\,\mathrm{cm}=2\,\mathrm{cm}</math></center> | ||
| + | |||
| + | ==Frecuencia de las oscilaciones== | ||
| + | Si consideramos el estado general de movimiento, tenemos las ecuaciones | ||
| + | |||
| + | <center><math>-k(\ell-\ell_0)-m_Ag+F_{T1}=m_Aa_A\qquad\qquad F_{T1}-m_Bg=m_B a_B = -m_Ba_A</math></center> | ||
| + | |||
| + | donde ahora <math>\ell</math> es una función del tiempo, como también lo es la tensión del hilo. Si sustituimos los valores numéricos queda | ||
| + | |||
| + | <center><math>-100(\ell-0.10)-3.5+F_{T1}=0.35a_A \qquad\qquad F_{T1}-6.5=-0.65a_A</math></center> | ||
| + | |||
| + | Restamos las ecuaciones | ||
| + | |||
| + | <center><math>1.0a_A=-100\ell + 10-3.5+6.5 = -100(\ell-0.13)</math></center> | ||
| + | |||
| + | Esta es la ecuación de un oscilador armónico, con posición de equilibrio, <math>\ell_\mathrm{eq}=0.13\,\mathrm{m}</math> y frecuencia | ||
| + | |||
| + | <math>\omega=\sqrt{\frac{100}{1.0}}=10\,\frac{\mathrm{rad}}{\mathrm{s}}</math> | ||
| + | |||
| + | ==Valor mínimo de la tensión== | ||
| + | Una vez que empieza a oscilar, la longitud del muelle varía como | ||
| + | |||
| + | <center><math>\ell=0.13+0.02\cos(10t)\,\qquad\qquad a_A=-2.0\cos(10t)</math></center> | ||
| + | |||
| + | lo que nos da la tensión en cada instante | ||
| + | |||
| + | <center><math>F_{T1}=6.5-0.65a_A=6.5+1.3\cos(10t)\,</math></center> | ||
| + | |||
| + | Por tanto, la tensión oscila entre su valor máximo inicial de 7.8N a un valor mínimo de 5.2N, no llegando a destensarse nunca. Para otros valores de las masas y longitudes de hilos sí es posible que este valor se haga 0 en cuyo caso el hilo se destensaria. | ||
última version al 02:57 2 ene 2006
Contenido |
1 Enunciado
Dos masas A y B, de masas 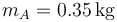 y
y 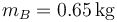 están unidas por un hilo ideal (“1”), inextensible y sin masa, que pasa por una polea ideal, sin masa ni rozamiento. La masa A está unida al suelo por un resorte de constante
están unidas por un hilo ideal (“1”), inextensible y sin masa, que pasa por una polea ideal, sin masa ni rozamiento. La masa A está unida al suelo por un resorte de constante 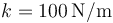 y longitud natural
y longitud natural 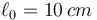 . La B se mantiene a la misma altura que la primera mediante otro hilo ideal (“2”) de 15 cm de longitud. El sistema está inicialmente en equilibrio.
. La B se mantiene a la misma altura que la primera mediante otro hilo ideal (“2”) de 15 cm de longitud. El sistema está inicialmente en equilibrio.

- ¿Cuánto vale la tensión de cada hilo?
- Suponga que se corta el hilo 2.
- ¿Cuánto vale la aceleración de cada masa justo tras el corte? ¿Y la tensión del hilo 1?
- ¿Cuánto mide la amplitud de las oscilaciones que describen las masas?
- ¿Cuál es la frecuencia ω de las oscilaciones que describe el sistema?
- Cuando el sistema está oscilando, ¿cuánto vale la tensión mínima del hilo? ¿Puede llegar a destensarse?
Tómese 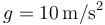 .
.
2 Tensiones
El equilibrio para la masa de la derecha da
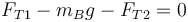
y para la de la izquierda

La fuerza elástica vale, teniendo en cuenta que el muelle mide 15cm

lo que da
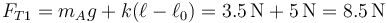
y
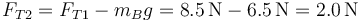
3 Situación tras el corte
Una vez que se corta el hilo, las masas comienza a moverse, aunque inicialmente sus posiciones siguen siendo las mismas. Esto quiere decir que, justo tras el corte, la fuerza ejercida por el resorte sigue siendo de 5.0 N. Ese muelle tira de la masa A hacia abajo, lo que hará subir a la B. Por la inextensibilidad del hilo
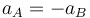
lo que nos da las ecuaciones de movimiento

con los valores numéricos

Restando las dos ecuaciones eliminamos la tensión

siendo la tensión justo después del corte
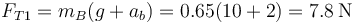
Nótese como el valor de la tensión cambia bruscamente al cortar el otro hilo. No puede suponerse que la tensión es la calculada para la posición inicial.
4 Amplitud de las oscilaciones
Puesto que las masas parten del reposo, la amplitud de las oscilaciones es la distancia entre la posición inicial, que ya conocemos, y la posición de equilibrio.
En la posición de equilibrio se cumple, para una masa
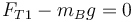
y para la otra
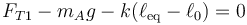
con valores numéricos


lo que nos da
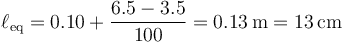
Dado que inicialmente, el muelle posee una elongación de 15 cm, la amplitud de las oscilaciones es
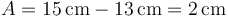
5 Frecuencia de las oscilaciones
Si consideramos el estado general de movimiento, tenemos las ecuaciones

donde ahora 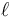 es una función del tiempo, como también lo es la tensión del hilo. Si sustituimos los valores numéricos queda
es una función del tiempo, como también lo es la tensión del hilo. Si sustituimos los valores numéricos queda

Restamos las ecuaciones

Esta es la ecuación de un oscilador armónico, con posición de equilibrio, 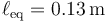 y frecuencia
y frecuencia
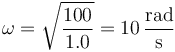
6 Valor mínimo de la tensión
Una vez que empieza a oscilar, la longitud del muelle varía como

lo que nos da la tensión en cada instante
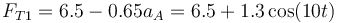
Por tanto, la tensión oscila entre su valor máximo inicial de 7.8N a un valor mínimo de 5.2N, no llegando a destensarse nunca. Para otros valores de las masas y longitudes de hilos sí es posible que este valor se haga 0 en cuyo caso el hilo se destensaria.





