Primera Prueba de Control 2019/20 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
Pedro (Discusión | contribuciones)
(Página creada con '== Masas con cuerda horizontal == right Las masas puntuales <math>m_1</math> y <math>m_2</mat…')
Edición más nueva →
(Página creada con '== Masas con cuerda horizontal == right Las masas puntuales <math>m_1</math> y <math>m_2</mat…')
Edición más nueva →
Revisión de 11:58 8 nov 2019
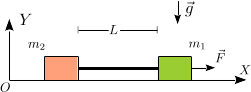
Masas con cuerda horizontal
Las masas puntuales m1 y m2 se deslizan sin rozamiento sobre una superficie horizontal.
Las masas están unidas por una cuerda ideal, inextensible y sin masa, de longitud L.
Una fuerza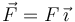 
actúa sobre la masa m1.
Las masas se mueven de modo que la cuerda está siempre tensa.
- Calcula la tensión de la cuerda durante el movimiento
- Supongamos ahora que las dos masas son iguales, m1 = m2 = m0. En el instante inicial la masa m2 esta en el punto O y la cuerda está completamente estirada. Las dos masas están en reposo en este instante inicial. Ahora la fuerza depende del tiempo como
, siendo A una constante.
- Cuáles son las unidades base de A en el S.I.
- ¿Cuál es la posición de la masa m1 en función del tiempo?
- En el instante t = tp la partícula 1 se para súbitamente. ¿Cuanto tiempo tarda en chocar con ella la partícula 2?
