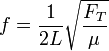Tensión de una cuerda de piano

(Diferencias entre revisiones)

Revisión de 13:12 12 mar 2009

Las cuerdas de los pianos están hechas esencialmente de acero (ρ = 7.85 g/cm&sup3) tensado

Determine la ecuación para la tensión de una cuerda si su diámetro es d y su longitud L y debe producir una nota de frecuencia f.
La nota más grave de un piano es el La de la subcontraoctava (27.5 Hz). Calcule la longitud que debería tener esta cuerda si está hecha de hilo de 1.224\,mm de diámetro y sometida a una tensión de 600 N. ¿Es factible esta longitud?
Si la longitud de la cuerda está limitada a 110 cm, ¿con qué tensión habría que tensar el hilo anterior para producir la misma nota?
Si la tensión debe ser 600 N y la longitud 110 cm, ¿qué grosor debería tener la cuerda para producir esta nota? ¿Cuál es el problema de este grosor?
Si un piano tiene un total de 200 cuerdas, ¿a qué tensión se encuentra la estructura del piano?

Las ondas estacionarias en una cuerda poseen una longitud de onda

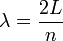
$\lambda = \frac{2L}{n}$

siendo la longitud correspondiente al modo fundamental el caso $n = 1$ , $λ = 2 L$ . La frecuencia correspondiente a esta longitud de onda es

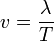
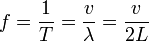
$v = \frac{\lambda}{T}$ $\Rightarrow$ $f = \frac{1}{T}=\frac{v}{\lambda}=\frac{v}{2L}$

Sustituyendo el valor de la velocidad para las ondas en una cuerda vibrante

$f = \frac{1}{2L}\sqrt{\frac{F_T}{\mu}}$

@@ Línea 10: / Línea 10: @@
 ==Solución==
 ===Solución general===
+Las ondas estacionarias en una cuerda poseen una longitud de onda
+<center><math>\lambda = \frac{2L}{n}</math></center>
+siendo la longitud correspondiente al modo fundamental el caso <math>n=1</math>, <math>\lambda = 2L</math>. La frecuencia correspondiente a esta longitud de onda es
+<center><math>v = \frac{\lambda}{T}</math>{{tose}}<math>f = \frac{1}{T}=\frac{v}{\lambda}=\frac{v}{2L}</math></center>
+Sustituyendo el valor de la velocidad para las ondas en una cuerda vibrante
+<center><math>f = \frac{1}{2L}\sqrt{\frac{F_T}{\mu}}</math></center>
 ===Longitud necesaria===
 ===Tensión necesaria===