Segunda Convocatoria Ordinaria 2018/19 (G.I.E.R.M.)
De Laplace
| Línea 12: | Línea 12: | ||
#Calcula la distancia <math>l</math> entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta. | #Calcula la distancia <math>l</math> entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta. | ||
#Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos <math>O</math> y <math>A</math>. | #Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos <math>O</math> y <math>A</math>. | ||
| - | #Calcula la potencia que la gravedad transmite a la partícula en cada Discute el significado físico del signo de esta potencia. | + | #Calcula la potencia que la gravedad transmite a la partícula en cada. Discute el significado físico del signo de esta potencia. |
#Calcula las componentes intrínsecas de la aceleración en el punto de impacto. | #Calcula las componentes intrínsecas de la aceleración en el punto de impacto. | ||
| Línea 47: | Línea 47: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | Cuando la partícula impacte con el plano inclinado se cumplirá | ||
| + | <center> | ||
| + | <math> | ||
| + | \overrightarrow{OA} = \vec{r}(t_i) | ||
| + | \Longrightarrow | ||
| + | \left\{ | ||
| + | \begin{array}{l} | ||
| + | \dfrac{4}{5}l = 6v_pt_i\\ | ||
| + | \\ | ||
| + | \dfrac{3}{5}l = 8v_pt_i - \dfrac{1}{2}gt_i^2 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | Tenemos dos ecuaciones para dos incógnitas: <math>l, t_i</math>. Resolviendo tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | t_A = \dfrac{v_p}{g}, \qquad l = \dfrac{105}{2}\dfrac{v_p^2}{g}. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | == Trabajo realizado por la gravedad == | ||
| + | El trabajo realizado por la fuerza gravitatoria es la variación de la energía potencial gravitatoria, con el signo cambiado | ||
| + | <center> | ||
| + | <math> | ||
| + | \Delta W_g = -\Delta U_g = -mgl\,\mathrm{sen}\,\theta = -\dfrac{63}{2}mv_p^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | == Potencia instantánea transmitida por la gravedad == | ||
| + | La potencia que, en cada instante, la fuerza gravitatoria comunica a la partícula es | ||
| + | <center> | ||
| + | <math> | ||
| + | P_g = \vec{F}_g\cdot\vec{v} = m\vec{g}\cdot\vec{v} = -g(8v_p-gt) | ||
| + | </math> | ||
| + | </center> | ||
| + | Esta potencia cambia de signo en el instante <math>t = 8v_p/g</math>. Sin embargo, este tiempo es menor que <math>t_i</math>. Entonces, durante todo el trayecto la potencia es negativa, es decir, la gravedad frena la partícula. | ||
Revisión de 06:03 24 ene 2006
Contenido |
1 Enunciado
Se tiene el plano inclinado de la figura que forma un ángulo θ con la horizontal. Se dispara una partícula desde el punto más bajo, con una velocidad inicial 
, de módulo 10vp y con un ángulo α con la horizontal. Los ángulos son tales que
- Calcula la distancia l entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
- Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos O y A.
- Calcula la potencia que la gravedad transmite a la partícula en cada. Discute el significado físico del signo de esta potencia.
- Calcula las componentes intrínsecas de la aceleración en el punto de impacto.
2 Solución
2.1 Impacto con el plano
La partícula se mueve únicamente bajo la acción de la graveda. Por tanto, su movimiento es un tiro parabólico. La posición y velocidad iniciales son
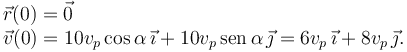
En el tiro oblicuo, el movimiento horizontal de la partícula es rectilíneo uniforme mientras que el vertical es uniformemente acelerado con aceleración − g. Los vectores aceleración, velocidad y posición de la partícula son
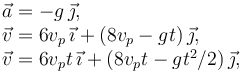
El vector de posición del punto A sobre la rampa es
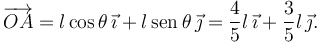
Cuando la partícula impacte con el plano inclinado se cumplirá
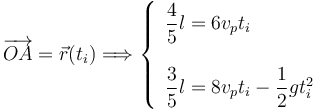
Tenemos dos ecuaciones para dos incógnitas: l,ti. Resolviendo tenemos
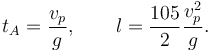
2.2 Trabajo realizado por la gravedad
El trabajo realizado por la fuerza gravitatoria es la variación de la energía potencial gravitatoria, con el signo cambiado
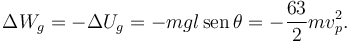
2.3 Potencia instantánea transmitida por la gravedad
La potencia que, en cada instante, la fuerza gravitatoria comunica a la partícula es
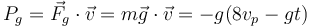
Esta potencia cambia de signo en el instante t = 8vp / g. Sin embargo, este tiempo es menor que ti. Entonces, durante todo el trayecto la potencia es negativa, es decir, la gravedad frena la partícula.
