Entrar Página Discusión Historial Go to the site toolbox

Momento de inercia de sólidos esféricos

De Laplace

(Diferencias entre revisiones)
(→Esfera hueca)
m (→Corona esférica)
Línea 48: Línea 48:
==Corona esférica==
==Corona esférica==
-
Cuando tenemos una corona esférica, de masa M, radio interior <math>R_1</math> y exterior <math>M_2</math>, podemos emplear la misma técnica que en otros problemas y considerar masas negativas.
+
Cuando tenemos una corona esférica, de masa M, radio interior <math>R_1</math> y exterior <math>R_2</math>, podemos emplear la misma técnica que en otros problemas y considerar masas negativas.
La corona esférica puede verse como la superposición de una esfera de radio <math>R_2</math> y densidad <math>+\rho</math> con una de radio <math>R_1</math>, densidad <math>-\rho</math>, concéntrica con la primera.
La corona esférica puede verse como la superposición de una esfera de radio <math>R_2</math> y densidad <math>+\rho</math> con una de radio <math>R_1</math>, densidad <math>-\rho</math>, concéntrica con la primera.

Revisión de 14:49 8 jul 2019

Contenido

1 Enunciado

Calcule el momento de inercia de una esfera maciza, de masa M y radio R alrededor de de un eje que pasa por su centro.

A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa M, radio interior R1 y exterior R2 respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio R?

2 Esfera maciza

Existen diferentes formas de abordar este problema, que es un clásico de cálculo integral.

Aquí lo haremos considerando la esfera como superposición de discos de espesor diferencial.

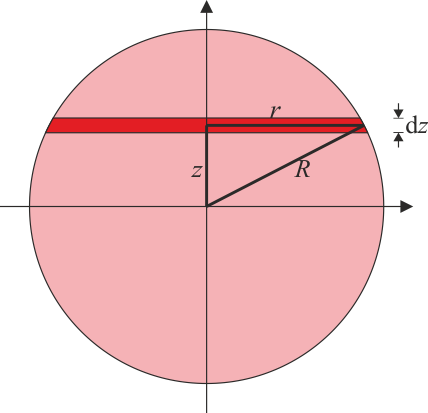
Archivo:momento-inercia-esferas-01.png

Si tenemos un disco de radio r, altura diferencial dz, su momento de inercia, también diferencial, es el correspondiente a un cilindro macizo

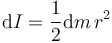
\mathrm{d}I = \frac{1}{2}\mathrm{d}m\,r^2

siendo la masa de cada disco el producto de la densidad por el volumen

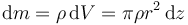
\mathrm{d}m = \rho\,\mathrm{d}V= \pi\rho r^2\,\mathrm{d}z

La densidad de una efsera maciza homogénea es igual a la masa total dividida por el volumen total

\rho = \frac{M}{4\pi R^3/3}=\frac{3M}{4\pi R^3}

lo que nos da el diferencial de masa

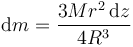
\mathrm{d}m = \frac{3M r^2\,\mathrm{d}z}{4 R^3}

y de momento de inercia

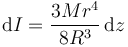
\mathrm{d}I = \frac{3M r^4}{8R^3}\,\mathrm{d}z

El momento de inercia total de la esfera será la suma de los de todos los discos apilados

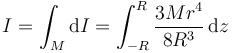
I = \int_M \mathrm{d}I = \int_{-R}^R \frac{3M r^4}{8R^3}\,\mathrm{d}z

En esta integral aparece el radio de cada disco, pero la variable de integración es la altura z a la que se encuentra cada uno (considerando el origen en el centro de la esfera). Estas dos cantidades se relacionan por el teorema de Pitágoras

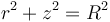
r^2+ z^2 = R^2\,

lo que nos deja con la integral

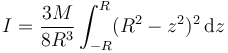
I=\frac{3M}{8R^3}\int_{-R}^R(R^2-z^2)^2\,\mathrm{d}z

con solución

I = \frac{2}{5}M R^2

3 Corona esférica

Cuando tenemos una corona esférica, de masa M, radio interior R1 y exterior R2, podemos emplear la misma técnica que en otros problemas y considerar masas negativas.

La corona esférica puede verse como la superposición de una esfera de radio R2 y densidad + ρ con una de radio R1, densidad − ρ, concéntrica con la primera.

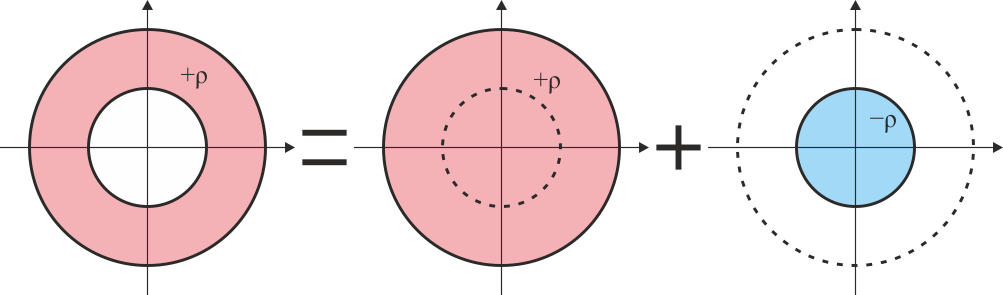
Archivo:momento-inercia-esferas-02.png

La masa de cada esfera sería

M_2 = \frac{4\pi}{3}\rho R_2^3\qquad \qquad M_1 = -\frac{4\pi}{3}\rho R_1^3

debiéndose cumplir que la masa total valga M

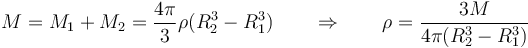
M = M_1 + M_2 = \frac{4\pi}{3}\rho (R_2^3-R_1^3) \qquad\Rightarrow\qquad \rho = \frac{3M}{4\pi(R_2^3-R_1^3)}

Los momentos de inercia de cada esfera valen, de la misma manera,

I_2=\frac{2}{5}M_2R_2^2 = \frac{8\pi}{15}\rho R_2^5\qquad \qquad I_1 = \frac{2}{5}M_1R_1^3 = -\frac{8\pi}{15}\rho R_1^5

Sumando las dos contribuciones hallamos el momento de inercia de la esfera completa

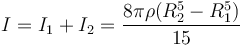
I=I_1+I_2= \frac{8\pi \rho (R_2^5-R_1^5)}{15}

Sustituimos aquí el valor de la densidad de masa

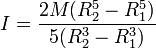
I = \frac{2M(R_2^5-R_1^5)}{5(R_2^3-R_1^3)}

4 Esfera hueca

La expresión anterior conduce a la de una esfera maciza sin más que hacer R1 = 0.

Para obtener el momento de inercia de una superficie esférica de masa M y radio R hay que ser más cuidadoso, ya que al hacer R1 = R2 = R aparece una indeterminación del tipo 0/0. Puede resolverse aplicando la regla de L'Hôpital

I = \lim_{R_1\to R}\frac{2M(R^5-R_1^5)}{5(R^3-R_1^3)}= \frac{2M}{5}\,\frac{(-5R^4)}{(-3R^2)}= \frac{2}{3}MR^2
Obtenido de "http://tesla.us.es/wiki/index.php/Momento_de_inercia_de_s%C3%B3lidos_esf%C3%A9ricos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace