Propiedades de una onda
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Solución) |
||
| Línea 15: | Línea 15: | ||
<center><math>\lambda = v\,T = 30\,\frac{\mathrm{m}}{\mathrm{s}}\,25\,\mathrm{ms}\,\frac{1\,\mathrm{s}}{1000\,\mathrm{ms}} = 0.75\,\mathrm{m}</math></center> | <center><math>\lambda = v\,T = 30\,\frac{\mathrm{m}}{\mathrm{s}}\,25\,\mathrm{ms}\,\frac{1\,\mathrm{s}}{1000\,\mathrm{ms}} = 0.75\,\mathrm{m}</math></center> | ||
| + | |||
| + | y de aquí el número de onda | ||
| + | |||
| + | <center><math>k = \frac{2\pi}{\lambda} = \frac{8\pi}{3}\,\mathrm{m}^{-1}</math></center> | ||
| + | |||
[[Categoría:Problemas de movimiento ondulatorio]] | [[Categoría:Problemas de movimiento ondulatorio]] | ||
Revisión de 13:35 9 mar 2009
1 Enunciado
Una onda sinusoidal transversal que se desplaza por una cuerda tiene un periodo T = 25.0 ms y viaja en la dirección negativa del eje x a una velocidad de 30 m/s. En el instante t = 0 s una partícula de la cuerda situada en la posición x = 0 m tiene un desplazamiento de 2.00 cm y se mueve hacia abajo con una velocidad de 2 m/s. Halle la amplitud, la longitud de onda, y el desfase inicial de esta señal.
2 Solución
La onda posee la expresión
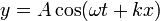
donde el signo "+" se debe a que viaja en la dirección negativa del eje x. La frecuencia angular ω la obtenemos del periodo

y, conocida el periodo y la velocidad de la onda obtenemos la longitud de onda
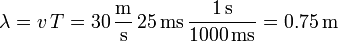
y de aquí el número de onda