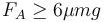Tren de dos ruedas (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un sistema está formado por dos discos homogéneos de masa m y radio R. Los discos están conectados mediante una varilla de masa despreciable y longitud 4R. Los …') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
Un sistema está formado por dos discos homogéneos de masa m y radio R. Los discos están conectados mediante una varilla de masa despreciable y longitud 4R. Los discos están unidos a la varilla mediante rodamientos que permiten el giro sin fricción. Ambos discos pueden rodar sin deslizar sobre una superficie horizontal en la que el coeficiente de rozamiento estático vale μ. Sea A el centro del disco delantero, B el del trasero, C el de contacto del disco delantero con el suelo y D el del trasero con el suelo. | Un sistema está formado por dos discos homogéneos de masa m y radio R. Los discos están conectados mediante una varilla de masa despreciable y longitud 4R. Los discos están unidos a la varilla mediante rodamientos que permiten el giro sin fricción. Ambos discos pueden rodar sin deslizar sobre una superficie horizontal en la que el coeficiente de rozamiento estático vale μ. Sea A el centro del disco delantero, B el del trasero, C el de contacto del disco delantero con el suelo y D el del trasero con el suelo. | ||
| - | <center>[[Archivo:Tren-dos-discos.png| | + | <center>[[Archivo:Tren-dos-discos.png|600px]]</center> |
Se tira del disco delantero mediante una fuerza constante horizontal <math>\vec{F}_A=F_A \vec{\imath}</math>. | Se tira del disco delantero mediante una fuerza constante horizontal <math>\vec{F}_A=F_A \vec{\imath}</math>. | ||
# Determine la aceleración de los centros de los dos discos cuando se ejerce esta fuerza. | # Determine la aceleración de los centros de los dos discos cuando se ejerce esta fuerza. | ||
# Halle el valor de las fuerzas sobre los discos en los puntos C y D, de contacto de estos con el suelo, así como la tensión de la varilla. | # Halle el valor de las fuerzas sobre los discos en los puntos C y D, de contacto de estos con el suelo, así como la tensión de la varilla. | ||
# Halle el máximo valor que puede tener F_A si no se desea que ninguno de los discos deslice. Si se alcanza este valor ¿Cuál es el primer disco que desliza, el delantero, el trasero, o ambos al mismo tiempo? | # Halle el máximo valor que puede tener F_A si no se desea que ninguno de los discos deslice. Si se alcanza este valor ¿Cuál es el primer disco que desliza, el delantero, el trasero, o ambos al mismo tiempo? | ||
| + | |||
==Aceleraciones== | ==Aceleraciones== | ||
<center><math>\vec{a}_A=\vec{a}_G=\frac{F_A}{3m}\vec{\imath}</math></center> | <center><math>\vec{a}_A=\vec{a}_G=\frac{F_A}{3m}\vec{\imath}</math></center> | ||
Revisión de 23:49 9 ene 2019
Contenido |
1 Enunciado
Un sistema está formado por dos discos homogéneos de masa m y radio R. Los discos están conectados mediante una varilla de masa despreciable y longitud 4R. Los discos están unidos a la varilla mediante rodamientos que permiten el giro sin fricción. Ambos discos pueden rodar sin deslizar sobre una superficie horizontal en la que el coeficiente de rozamiento estático vale μ. Sea A el centro del disco delantero, B el del trasero, C el de contacto del disco delantero con el suelo y D el del trasero con el suelo.

Se tira del disco delantero mediante una fuerza constante horizontal 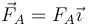 .
.
- Determine la aceleración de los centros de los dos discos cuando se ejerce esta fuerza.
- Halle el valor de las fuerzas sobre los discos en los puntos C y D, de contacto de estos con el suelo, así como la tensión de la varilla.
- Halle el máximo valor que puede tener F_A si no se desea que ninguno de los discos deslice. Si se alcanza este valor ¿Cuál es el primer disco que desliza, el delantero, el trasero, o ambos al mismo tiempo?
2 Aceleraciones
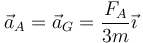
3 Fuerzas


4 Deslizamiento inminente