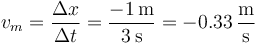Posición dependiente del tiempo (GIE)
De Laplace
(Diferencias entre revisiones)
m (→Distancia recorrida) |
|||
| Línea 11: | Línea 11: | ||
<center><math>\Delta x = x(4\,\mathrm{s})-x(0\,\mathrm{s})=-1\,\mathrm{m}-1\,\mathrm{m}=-2\,\mathrm{m}</math></center> | <center><math>\Delta x = x(4\,\mathrm{s})-x(0\,\mathrm{s})=-1\,\mathrm{m}-1\,\mathrm{m}=-2\,\mathrm{m}</math></center> | ||
==Distancia recorrida== | ==Distancia recorrida== | ||
| - | Es la suma de la que avanza hasta t | + | Es la suma de la que avanza hasta <math>t=2\,\mathrm{s}</math> y la que retrocede desde ese momento |
<center><math>\Delta s = |x(2\,\mathrm{s})-x(0\,\mathrm{s})|+|x(4\,\mathrm{s})-x(2\,\mathrm{s})|=(1+3)\,\mathrm{m}=4\,\mathrm{m}</math></center> | <center><math>\Delta s = |x(2\,\mathrm{s})-x(0\,\mathrm{s})|+|x(4\,\mathrm{s})-x(2\,\mathrm{s})|=(1+3)\,\mathrm{m}=4\,\mathrm{m}</math></center> | ||
| + | |||
==Desplazamiento y distancia== | ==Desplazamiento y distancia== | ||
última version al 16:47 8 oct 2018
Contenido |
1 Enunciado
Una partícula se mueve de manera que su posición como función del tiempo está representada en la gráfica de la figura
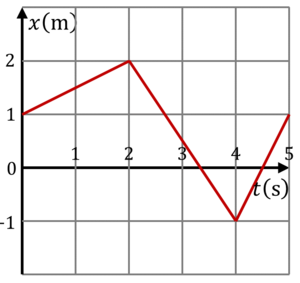
- ¿Cuánto vale su desplazamiento entre
y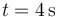 
?
- ¿Cuánto vale la distancia total recorrida en el mismo intervalo?
- ¿Cuánto vale el desplazamiento y la distancia total recorrida en el intervalo (0 s,5 s)?
- ¿Cuánto vale la velocidad media en los intervalos (0 s,5 s), (0 s,4 s) y (2 s,5 s)?
- ¿Cómo es la gráfica de la velocidad instantánea como función del tiempo?
2 Desplazamiento
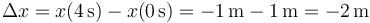
3 Distancia recorrida
Es la suma de la que avanza hasta 
y la que retrocede desde ese momento
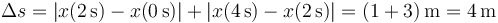
4 Desplazamiento y distancia
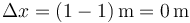
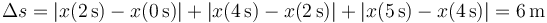
5 Velocidades medias
5.1 Entre 0s y 5s
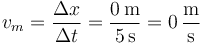
5.2 Entre 0 y 4s
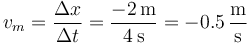
5.3 Entre 2 y 5 s
