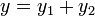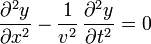Superposición de ondas
De Laplace
(Diferencias entre revisiones)
(→Introducción) |
|||
| Línea 6: | Línea 6: | ||
(esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución | (esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución | ||
| - | <center><math>y=y_1+y_2</math>{{tose}}<math>\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0</math></center> | + | <center><math>y=y_1+y_2\,</math>{{tose}}<math>\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0</math></center> |
==Mismo sentido== | ==Mismo sentido== | ||
Revisión de 18:51 25 feb 2009
Contenido |
1 Introducción
Una de las propiedades de la ecuación de onda es que se trata de una ecuación lineal, esto quiere decir que admite el principio de superposición. Esto significa que si y1 e y2 son las soluciones de la misma ecuación de onda
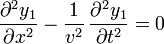
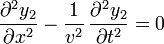
(esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución