Péndulo cónico (CMR)
De Laplace
(Diferencias entre revisiones)
| Línea 2: | Línea 2: | ||
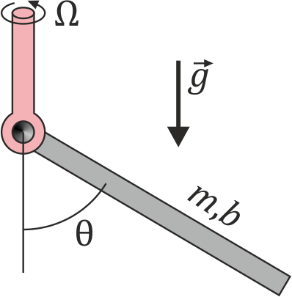
Una barra homogénea de masa <math>m</math> y longitud <math>b</math> se encuentra articulada en su extremo <math>O</math> a un eje vertical que gira con velocidad angular constante <math>\vec{\omega}_{21}=\Omega\vec{k}_1</math>. La barra mantiene en su giro un ángulo constante con la vertical. Determine este ángulo en función de Ω y del resto de constantes del problema. ¿Se levanta la barra para todas las velocidades de giro? ¿Qué velocidad angular se necesita para que la barra quede completamente horizontal? | Una barra homogénea de masa <math>m</math> y longitud <math>b</math> se encuentra articulada en su extremo <math>O</math> a un eje vertical que gira con velocidad angular constante <math>\vec{\omega}_{21}=\Omega\vec{k}_1</math>. La barra mantiene en su giro un ángulo constante con la vertical. Determine este ángulo en función de Ω y del resto de constantes del problema. ¿Se levanta la barra para todas las velocidades de giro? ¿Qué velocidad angular se necesita para que la barra quede completamente horizontal? | ||
<center> | <center> | ||
| + | |||
| + | [[Archivo:barra-pendulo-conico.png]]</center> | ||
==Sistemas de referencia== | ==Sistemas de referencia== | ||
==Ecuaciones de movimiento== | ==Ecuaciones de movimiento== | ||
==Caso general== | ==Caso general== | ||
| - | [[ | + | [[Categoría:Problemas de dinámica del sólido rígido (CMR)]] |
última version al 10:36 30 ago 2018
Contenido |
1 Enunciado
Una barra homogénea de masa m y longitud b se encuentra articulada en su extremo O a un eje vertical que gira con velocidad angular constante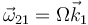 
. La barra mantiene en su giro un ángulo constante con la vertical. Determine este ángulo en función de Ω y del resto de constantes del problema. ¿Se levanta la barra para todas las velocidades de giro? ¿Qué velocidad angular se necesita para que la barra quede completamente horizontal?
