Entrar Página Discusión Historial Go to the site toolbox

Conductor cúbico con placas enfrentadas (GIE)

De Laplace

(Diferencias entre revisiones)
(→Potencial del cubo)
(→Potencial del cubo)
Línea 20: Línea 20:
<center><math>C_0=\frac{\varepsilon b^2}{a}=\frac{2\times 10^{-11}(0.1)^2}{0.001}=200\,\mathrm{pF}</math></center>
<center><math>C_0=\frac{\varepsilon b^2}{a}=\frac{2\times 10^{-11}(0.1)^2}{0.001}=200\,\mathrm{pF}</math></center>
-
<center>[[Archivo:circuito-cubo.png]]</center>
+
<center>[[Archivo:circuito-cubo.png|500px]]</center>
El voltaje al que se encuentra el cubo es <math>V_c</math>, desconocido por ahora, mientras que las placas exteriores se hallan a voltajes <math>V_i</math>, siendo desconocida su carga.
El voltaje al que se encuentra el cubo es <math>V_c</math>, desconocido por ahora, mientras que las placas exteriores se hallan a voltajes <math>V_i</math>, siendo desconocida su carga.

Revisión de 07:35 23 jun 2018

Contenido

1 Enunciado

Se tiene un sistema de conductores formado por un bloque central de forma cúbica, de arista 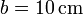b=10\,\mathrm{cm}. Este bloque está forrado por una capa de dieléctrico de espesor 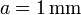a=1\,\mathrm{mm}, siendo \varepsilon=2\times 10^{-11} \mathrm{F}/\mathrm{m} la permitividad del dieléctrico. Frente a cada cara del cubo y pegadas al dieléctrico se hallan 6 placas conductoras de lado b. El cubo central está aislado y descargado. Cada una de las placas tiene su tensión fijada por una fuente o una conexión a tierra. Numeramos las caras como las de un dado. La placa 1 está a un voltaje de 9 V, la 2 (contigua a la 1) a 3 V y la 3 (contigua a la 1 y a la 2) a 6 V. La placa 4 (opuesta a la 3), la 5 (opuesta a la 2) y la 6 (opuesta a la 1) están a tierra.

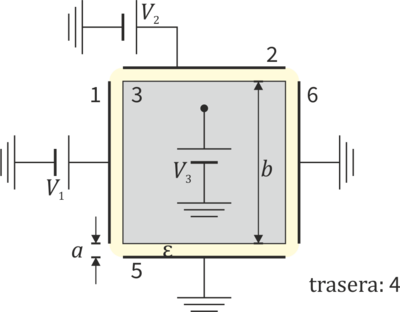
Halle:

  1. El voltaje al que se encuentra el cubo central.
  2. La carga de cada una de las placas exteriores.
  3. La energía electrostática almacenada en el sistema.

Suponga que la placa 3 se desconecta de su fuente y se pone a tierra.

  1. ¿Cuánto cambia la energía del sistema?
  2. ¿Qué trabajo realiza cada uno de los generadores 1 y 2?

Despréciense los efectos de borde, de manera que el para formado por cada placa y la cara correspondiente del cubo puede tratarse como un condensador plano.

2 Potencial del cubo

El circuito equivalente está formado por un nodo central (el cubo) conectado a 6 condensadores iguales de capacidad

C_0=\frac{\varepsilon b^2}{a}=\frac{2\times 10^{-11}(0.1)^2}{0.001}=200\,\mathrm{pF}

El voltaje al que se encuentra el cubo es Vc, desconocido por ahora, mientras que las placas exteriores se hallan a voltajes Vi, siendo desconocida su carga.

La carga de la esfera central es la suma de las de las seis caras, cada una de las cuales se halla como la del condensador correspondiente

0 = C_0(V_c-V_1)+C_0(V_c-V_2)+\cdots

siendo V1, V2, … los voltajes de las placas exteriores. Igualando a 0 y despejando resulta la media aritmética de estos voltajes

0=C_0(6V_c-V_1-V_2-\cdots)\qquad\Rightarrow\qquad V_c=\frac{V_1+V_2+V_3+V_4+V_5+V_6}{6}

En este caso

V_c=\frac{9+3+6+0+0+0}{6}\,\mathrm{V}=3\,\mathrm{V}

3 Carga de las placas

Cada una es la de un condensador.

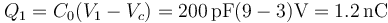
Q_1=C_0(V_1-V_c)=200\,\mathrm{pF}(9-3)\mathrm{V}=1.2\,\mathrm{nC}

 

Q_2=C_0(V_2-V_c)=200\,\mathrm{pF}(3-3)\mathrm{V}=0.0\,\mathrm{nC}

 

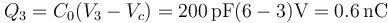
Q_3=C_0(V_3-V_c)=200\,\mathrm{pF}(6-3)\mathrm{V}=0.6\,\mathrm{nC}

 

Q_4=Q_5=Q_6=C_0(V_4-V_c)=200\,\mathrm{pF}(0-3)\mathrm{V}=-0.6\,\mathrm{nC}

4 Energía almacenada

Para un sistema de conductores

U_\mathrm{e}=\frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2+\cdots

De los siete conductores (las seis placas y el cubo) hay tres a potencial nulo (las placas 4, 5 y 6) y dos (el cubo y la placa 2) con carga nula. Los únicos que contribuyen a la energía son la placa 1 y la 3

U_\mathrm{e}=\frac{1}{2}(1.2\,\mathrm{nC})(9\mathrm{V})+\frac{1}{2}(0.6\,\mathrm{nC})(6\mathrm{V})=7.2\,\mathrm{nJ}

5 Tras la conexión

5.1 Energía almacenada

Tras la conexión de la placa 3 a tierra, el nuevo voltaje del cubo es

V'_c=\frac{9+3+0+0+0+0}{6}\mathrm{V}=2\,\mathrm{V}

y las nuevas cargas de las placas valen

Q'_1=C_0(V_1-V'_c)=200\,\mathrm{pF}(9-2)\mathrm{V}=1.4\,\mathrm{nC}

 

Q'_2=C_0(V_2-V'_c)=200\,\mathrm{pF}(3-2)\mathrm{V}=0.2\,\mathrm{nC}

 

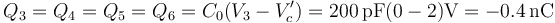Q_3=Q_4=Q_5=Q_6=C_0(V_3-V'_c)=200\,\mathrm{pF}(0-2)\mathrm{V}=-0.4\,\mathrm{nC}</cen}ter>

Esto nos da la nueva energía

<center>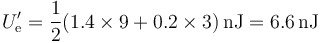U'_\mathrm{e}=\frac{1}{2}(1.4\times 9+0.2\times 3)\,\mathrm{nJ}=6.6\,\mathrm{nJ}

5.2 Trabajo de los generadores

El trabajo de cada generador es

W_g=V_g\,\Delta Q

Para el generador 1

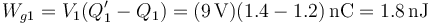
W_{g1}=V_1(Q'_1-Q_1)=(9\,\mathrm{V})(1.4-1.2)\,\mathrm{nC}=1.8\,\mathrm{nJ}

Para el 2

W_{g1}=V_2(Q'_2-Q_2)=(3\,\mathrm{V})(0.0-0.2)\,\mathrm{nC}=-0.6\,\mathrm{nJ}

En total los generadores realizan 1.2nJ, pero la energía almacenada baja en 0.6nJ, luego se pierden 1.8nJ

Obtenido de "http://tesla.us.es/wiki/index.php/Conductor_c%C3%BAbico_con_placas_enfrentadas_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace