De Laplace

(Diferencias entre revisiones)

Revisión de 18:08 29 may 2018

Contenido

1 Introducción
2 Coordenadas generalizadas
- 2.1 Partícula puntual
- 2.2 Sistemas de partículas: Sólido Rígido
3 Ligaduras
- 3.1 Ligaduras holónomas
- 3.2 Ligaduras no holónomas

1 Introducción

En los temas anteriores hemos visto como se aplican los principios de la Mecánica Vectorial al estudio del Sólido Rígido. En Mecánica Vectorial las magnitudes que describen el movimiento del sistema son la Cantidad de Movimiento y el Momento Cinético. Y las acciones sobre un Sólido Rígido se describen utilizando fuerzas y pares de fuerzas. Todas estas magnitudes son vectores, de ahí su nombre. El Teorema del Centro de Masas y el Teorema del Momento Cinético proporcionan las ecuaciones diferenciales del movimiento. Estas ecuaciones también son vectoriales.

En Mecánica Analítica, en cambio, la dinámica de los sistemas de partículas se describe usando magnitudes escalares: la energía cinética, la energía potencial, la función de Lagrange, etc. Esto no quiere decir que los vectores no aparezcan. Las acciones sobre un Sólido Rígido todavía se describen usando vectores y pares de fuerzas, especialmente en el caso de sistemas no conservativos. Pero el objetivo será encontrar la función de Lagrange del sistema (un escalar) y a partir de ella encontrar las ecuaciones del movimiento.

La Mecánica Analítica describe el estado de un sistema a través de coordenadas generalizadas. Al analizar un problema el primer paso es identificar las coordenadas generalizadas mas adecuadas y el número mínimo necesario para describir el sistema: el número de grados de libertad. Esto permitirá, en general, eliminar las fuerzas de ligadura del problema. Cualquier magnitud física puede ser una coordenada generalizada: una distancia, un ángulo, una componente de fuerza, etc. En ingeniería serán casi siempre distancias y ángulos.

La Mecánica Analítica es muy potente. Permite encontrar con relativa facilidad las condiciones de equilibrio y las ecuaciones de movimiento de sistemas muy complejos. A cambio, requiere un grado mayor de abstracción en el tratamiento de los problemas.

2 Coordenadas generalizadas

2.1 Partícula puntual

Consideremos el sistema mecánico mas sencillo posible: un partícula puntual libre de masa $m$ . Usando coordenadas cartesianas la posición de la partícula en cada instante de tiempo puede describirse usando su vector de posición respecto a un cierto sistema de ejes coordenados:

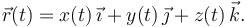
$\vec{r}(t) = x(t)\,\vec{\imath} + y(t)\,\vec{\jmath} + z(t)\,\vec{k}.$

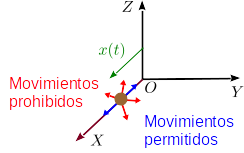
Que la partícula sea libre significa que las tres coordenadas ${x, y, z}$ pueden tomar cualquier valor independientemente de las otras. Entonces, no hay ningún movimiento prohibido para la partícula, como se indica en la figura. El número de grados de libertad es 3.

Supongamos ahora que la partícula está obligada a moverse en el eje $O X$ .Podemos imaginar que la partícula es una cuenta engarzada en un alambre recto y hacemos coincidir el eje $O X$ con el alambre. Esto significa que, no importa la fuerza que ejerzamos sobre la partícula, esta no puede salirse del hilo. Cualquier movimiento que la saque del hilo está prohibido. Se dice entonces que la partícula está vinculada o ligada. Entonces, no necesitamos las tres coordenadas cartesianas para determinar la posición de la partícula. Sabemos que se cumplirá siempre $y (t) = 0$ y $z (t) = 0$ : estas condiciones se llaman ligaduras o vínculos. La partícula tiene un grado de libertad y podemos elegir como coordenada $x (t)$ . El vector de posición sería

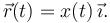
$\vec{r}(t) = x(t)\,\vec{\imath}.$

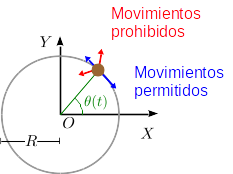
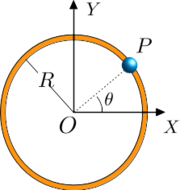
Supongamos que el hilo es circular, de radio $R$ y situado en el plano $z = 0$ . El vector de posición de la partícula es

$\vec{r}(t) = x(t)\,\vec{\imath} + y(t)\,\vec{\jmath}.$

Vemos dos coordenadas en el vector: ${x, y}$ , pero la partícula tiene sólo un grado de libertad. Lo que ocurre es que estas coordenadas no pueden variar de forma independiente. Tienen que cumplir la ligadura $x 2 + y 2 = R 2$ . Podríamos escoger $x$ o $y$ para especificar la posición de la partícula y despejar la otra a partir de la condición de ligadura. Pero en este caso es mas conveniente escoger el ángulo de la figura como coordenada: ${θ}$ . De esta forma el vector de posición es

$\vec{r}(t) = R\cos\theta(t)\,\vec{\imath} + R\,\mathrm{sen}\,\theta(t)\,\vec{\jmath}.$

En el caso de la figura la partícula tiene dos grados de libertad. Podemos expresar el vector de posición en función de $r (t)$ y $θ(t)$

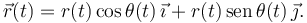
$\vec{r}(t) = r(t)\cos\theta(t)\,\vec{\imath} + r(t)\,\mathrm{sen}\,\theta(t)\,\vec{\jmath}.$

El número de grados de libertad es 2 y las coordenadas usadas son ${r,θ}$ .

En este último caso hemos usado un ángulo y una distancia para describir la posición de la partícula, aunque sean magnitudes cualitativamente distintas. Este es el concepto de coordenadas generalizadas: son cualesquiera magnitudes pueden utilizarse para describir un sistema. En este curso serán distancias y/o ángulos, pero en general puede ser cualquier cosa: una componente de momento de una fuerza, un índice bursátil, etc.

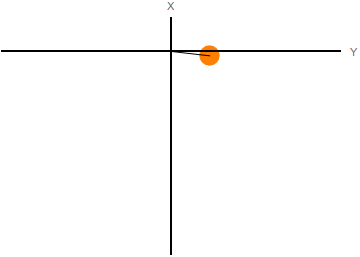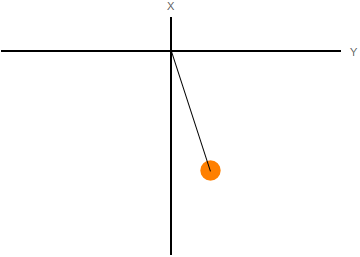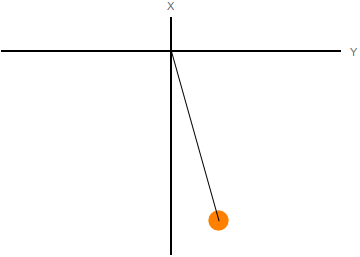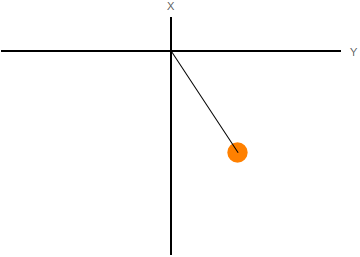
El espacio de configuraciones es el generado por las coordenadas generalizadas. El movimiento del sistema puede visualizarse como el movimiento de un punto que representa al sistema en el espacio de las configuraciones. En la figura de la izquierda representamos el movimiento del péndulo con muelle del último ejemplo en el espacio real. A la derecha se representa el movimiento de la masa en el espacio de las configuraciones.

2.2 Sistemas de partículas: Sólido Rígido

Si tenemos un sistema con $N$ partículas, tendremos $N$ vectores de posición 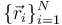$\{\vec{r}_i\}_{i=1}^N$ y, por tanto, $3 N$ coordenadas cartesianas. Si las partículas tienen que cumplir $k$ ligaduras, el número de grados de libertad es $n = 3 N - k$ . Necesitaremos entonces $n$ coordenadas generalizadas, $\{q_k(t)\}_{k=1}^n$ , para describir en cada instante la configuración del sistema.

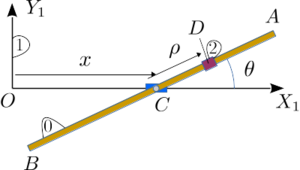
En el caso de un sólido rígido libre ya hemos visto que se necesitan 6 coordenadas para describir su posición: 3 coordenadas asociadas a la traslación y 3 a la rotación. Aunque un sólido tiene muchos puntos, la condición de rigidez impone condiciones muy restrictivas al movimiento, resultando en 6 grados de libertad para el sólido rígido libre. En el caso de sólidos vinculados habrá que examinar cada sistema individualmente. Por ejemplo, el sistema de la figura, formado por dos sólidos vinculados, tiene 3 grados de libertad

$\{q_1 = x, q_2=\theta, q_3=\rho\} \qquad n=3.$

3 Ligaduras

Como hemos visto en el apartado anterior, las restricciones al movimiento en sistemas mecánicos reciben el nombre de ligaduras o vínculos. Hay varias formas de clasificar las ligaduras. En Mecánica Analítica, la distinción mas importante es entre ligaduras holónomas y no holónomas.

3.1 Ligaduras holónomas

Son ligaduras que pueden expresarse por una relación matemática que involucre sólamante las coordenadas geométricas y, quizás, el tiempo. Si el sistema tiene $N$ partículas

$f(x_1, x_2, \ldots, x_{3N},t)=0$

Como vemos las velocidades no aparecen en la expresión. Si el tiempo no aparece explícitamente en la expresión se llaman esclerónomas. Si el tiempo sí aparece explícitamente se llaman reónomas.

Veamos algunos ejemples, con su denominación particular

Geométricas bilaterales

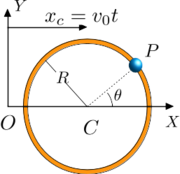
Establece una relación de igualdad entre las coordenadas. Por ejemplo, una partícula engarzada en una circunferencia de radio $R$ centrada en el origen y en el plano $O X Y$ es un ejemplo de ligaduras holónomas geométricas bilaterales y esclerónomas

$\begin{array}{l} z=0\\x^2+y^2=R^2. \end{array}$

Si el aro se mueve con una velocidad prefijada, como se indica en la figura, el tiempo aparece explícitamente en la segunda ligadura, que pasa a ser reónoma.

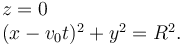
$\begin{array}{l} z=0\\(x-v_0t)^2+y^2=R^2. \end{array}$

Si una de las ligaduras es reónoma el sistema entero se denomina reónomo. En muchas ocasiones las ligaduras reónomas corresponden a vínculos con un movimiento prefijado.

Cinématicas integrables

Las ligaduras cinemáticas son aquellas en las que se imponen condiciones sobre alguna o todas las velocidades. Su forma general es

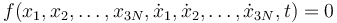
$f(x_1, x_2, \ldots, x_{3N},\dot{x}_1, \dot{x}_2, \ldots, \dot{x}_{3N},t)=0$

Si la expresión puede integrarse para eliminar las velocidades se convierte en una ligadura geómetrica bilateral. Por tanto es holónoma.

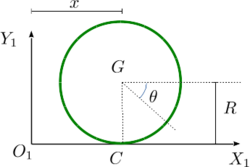
Un ejemplo muy importante en Ingeniería es la rodadura sin deslizamiento en un movimiento plano. Para el aro de radio $R$ de la izquierda tenemos

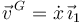
$\vec{v}^{\,G} = \dot{x}\,\vec{\imath}_1$

La condición de rodadura sin deslizamiento impone 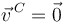$\vec{v}^{\,C}=\vec{0}$ . Usando el Teorema de Chasles

$\vec{v}^{\,G} = \vec{v}^{\,C} + \vec{\omega}\times\overrightarrow{CG} \Longrightarrow \dot{x} = R\,\dot{\theta}.$

Esta es una ligadura cinemática, pues involucra a derivadas temporales de las coordenadas generalizadas. Pero puede integrarse. La ligadura puede expresarse como

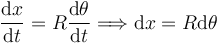
$\dfrac{\mathrm{d}x}{\mathrm{d}t} = R\dfrac{\mathrm{d}\theta}{\mathrm{d}t} \Longrightarrow \mathrm{d}x = R\mathrm{d}\theta$

Esta expresión puede integrarse

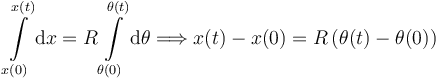
$\int\limits_{x(0)}^{x(t)}\mathrm{d}x = R\int\limits_{\theta(0)}^{\theta(t)}\mathrm{d}\theta \Longrightarrow x(t) - x(0) = R\,(\theta(t)-\theta(0))$

Obtenemos así una ligadura holónoma.

3.2 Ligaduras no holónomas

En este caso no pueden expresarse con una relación matemática de la forma $f(x_1, x_2, \ldots, x_{3N},t)=0$ . Veamos algunos ejemplos

Geométricas unilaterales

La expresión matemática del vínculo es una inegualdad que involucra a las coordenadas y, quizás, el tiempo. Por ejemplo, para una partícula botando en una mesa, de modo que el plano de la mesa es el plano $O X Y$ , la ligadura es

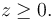
$z\geq0.$

Este ligadura es esclerónoma. Si la mesa se mueve con velocidad vertical uniforme $v 0$ la ligadura sería (suponiendo que en $t = 0$ la mesa coincide con el plano $O X Y$ )

$z\geq v_0t.$

Esta ligadura es reónoma.

Rodadura sin deslizamiento en 3D

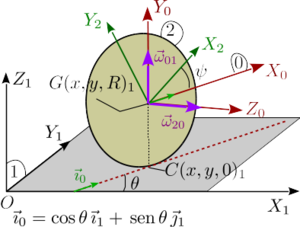
Supongamos que tenemos un disco de radio $R$ que rueda sin deslizar y pivota sobre una superficie plana, pero sin tumbarse. Podemos imaginar una moneda rodando en el suelo. Escogemos como sólido "0" un triedro cuyo origen se mueve con el centro del disco, $G$ , y el eje $G Z 0$ es siempre perpendicular al disco. El triedro "2", solidario con el disco, tiene como origen su centro y su eje $G Z 2$ coincide en todo momento con el $G Z 0$ . Las coordenadas generalizadas son las coordenadas cartesianas del centro del disco, $x, y$ , el ángulo $θ$ que forma el eje $G X 0$ con el eje fijo $O X 1$ , y el ángulo $ψ$ que forma el eje $G X 2$ con el eje $G X 0$ . Podría parecer en principio que hay 4 grados de libertad, pero sólo hay 2. Esto puede razonarse así. Un sólido rígido libre tiene 6 grados de libertad. La condición de rodadura sin deslizamiento imponte 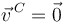$\vec{v}^{\,C}=\vec{0}$ (3 vínculos cinemáticos). Si no puede tumbarse hay una componente prohibida de la rotación. Así pues, el número de grados de libertad es $n = 6 - 4 = 2$ . Veamos como se obtienen las expresiones de las ligaduras.

Para el movimiento {01} tenemos

$\begin{array}{l} \vec{\omega}_{01} = \dot{\theta}\,\vec{k}_1,\\ \vec{v}^{\,G}_{01} = \dot{x}\,\vec{\imath}_1 + \dot{y}\,\vec{\jmath}_1,\\ \vec{v}^{\,C}_{01} = \vec{v}^{\,G}_{01} + \vec{\omega}_{01}\times\overrightarrow{GC} = \dot{x}\,\vec{\imath}_1 + \dot{y}\,\vec{\jmath}_1. \end{array}$

Para el {20}

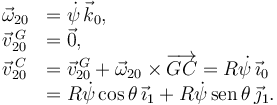
$\begin{array}{ll} \vec{\omega}_{20} & = \dot{\psi}\,\vec{k}_0,\\ \vec{v}^{\,G}_{20}& = \vec{0},\\ \vec{v}^{\,C}_{20}& = \vec{v}^{\,G}_{20} + \vec{\omega}_{20}\times\overrightarrow{GC} =R\dot{\psi}\,\vec{\imath}_0\\ & = R\dot{\psi}\cos\theta\,\vec{\imath}_1 + R\dot{\psi}\,\mathrm{sen}\,\theta\,\vec{\jmath}_1. \end{array}$

La rodadura sin deslizamiento impone 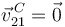$\vec{v}^{\,C}_{21}=\vec{0}$ . Entonces

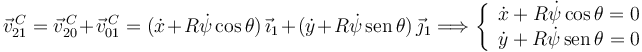
$\vec{v}^{\,C}_{21} = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} = (\dot{x} + R\dot{\psi}\cos\theta)\,\vec{\imath}_1 + (\dot{y} + R\dot{\psi}\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1 \Longrightarrow \left\{ \begin{array}{l} \dot{x} + R\dot{\psi}\cos\theta=0\\ \dot{y} + R\dot{\psi}\,\mathrm{sen}\,\theta=0 \end{array} \right.$

Estas ligaduras no se pueden integrar. Por ejemplo, la primera puede manipularse así

$\dfrac{\mathrm{d}x}{\mathrm{d}t} = -R\cos\theta\dfrac{\mathrm{d}\psi}{\mathrm{d}t} \Longrightarrow \int\mathrm{d}x = R\int\cos\theta\,\mathrm{d}\psi.$

La segunda integral no se puede hacer, pues $θ$ no es constante durante el movimiento y no sabemos como depende de $ψ$ . Este es un caso en el que hay que describir el sistema con cuatro coordenadas generalizadas, ${x, y,θ,ψ}$ , aunque haya sólo dos grados de libertad. Veremos mas adelante que hay técnicas para tratar este tipo de problemas.

@@ Línea 182: / Línea 182: @@
 ; Rodadura sin deslizamiento en 3D
 Supongamos que tenemos un disco de radio <math>R</math> que rueda sin deslizar
-y pivota sobre una superficie plana. Podemos imaginar una moneda rodando en el suelo.
+y pivota sobre una superficie plana, pero sin tumbarse. Podemos imaginar una moneda rodando en el suelo.
 Escogemos como sólido "0" un triedro cuyo origen se mueve con el centro del
 disco, <math>G</math>, y el eje <math>GZ_0</math> es siempre perpendicular al disco.
 El triedro "2",
 solidario con el disco, tiene como origen su centro y su eje <math>GZ_2</math> coincide en todo momento con el <math>GZ_0</math>. Las coordenadas generalizadas son las
-coordenadas cartesianas del centro del disco, <math>x, y</math>, el ángulo <math>\theta</math> que forma el eje <math>GX_0</math> con el eje fijo <math>OX_1</math>, y el ángulo <math>\psi</math> que forma el eje <math>GX_2</math> con el eje <math>GX_0</math>. Podría parecer en principio que hay 4 grados de libertad, pero sólo hay 3. Esto
+coordenadas cartesianas del centro del disco, <math>x, y</math>, el ángulo <math>\theta</math> que forma el eje <math>GX_0</math> con el eje fijo <math>OX_1</math>, y el ángulo <math>\psi</math> que forma el eje <math>GX_2</math> con el eje <math>GX_0</math>. Podría parecer en principio que hay 4 grados de libertad, pero sólo hay 2. Esto
-puede razonarse así. Un sólido rígido libre tiene 6 grados de libertad. La condición de que el disco se mueve sobre el plano impone que la componente vertical de la velocidad absoluta del centro del disco es cero (vínculo cinemático). Además, la rodadura sin deslizamiento imponte <math>\vec{v}^{\,C}=\vec{0}</math> (2 vínculos cinemáticos, la velocidad vertical ya es cero por el vínculo anterior). Así pues, el número de grados de libertad es <math>n = 6-3=3</math>. Veamos como se obtienen las expresiones de las ligaduras.
+puede razonarse así. Un sólido rígido libre tiene 6 grados de libertad. La condición de  rodadura sin deslizamiento imponte <math>\vec{v}^{\,C}=\vec{0}</math> (3 vínculos cinemáticos). Si no puede tumbarse hay una componente prohibida de la rotación.
+Así pues, el número de grados de libertad es <math>n = 6-4=2</math>. Veamos como se obtienen las expresiones de las ligaduras.
 [[Archivo:MR_09_09.png|right|300px]]
@@ Línea 205: / Línea 206: @@
 <center>
 <math>
-\begin{array}{l}
+\begin{array}{ll}
-\vec{\omega}_{20} = \dot{\psi}\,\vec{k}_0,\\
+\vec{\omega}_{20} & = \dot{\psi}\,\vec{k}_0,\\
-\vec{v}^{\,G}_{20} = \vec{0},\\
+\vec{v}^{\,G}_{20}& = \vec{0},\\
-\vec{v}^{\,C}_{20} = \vec{v}^{\,G}_{20} + \vec{\omega}_{20}\times\overrightarrow{GC}
+\vec{v}^{\,C}_{20}& = \vec{v}^{\,G}_{20} + \vec{\omega}_{20}\times\overrightarrow{GC}
-=R\dot{\psi}\,\vec{\imath}_0 = R\dot{\psi}\cos\theta\,\vec{\imath}_1
+=R\dot{\psi}\,\vec{\imath}_0\\
+& = R\dot{\psi}\cos\theta\,\vec{\imath}_1
 + R\dot{\psi}\,\mathrm{sen}\,\theta\,\vec{\jmath}_1.
 \end{array}
 </math>
 </center>
+La rodadura sin deslizamiento impone <math>\vec{v}^{\,C}_{21}=\vec{0}</math>. Entonces
+<center>
+<math>
+\vec{v}^{\,C}_{21} = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} =
+(\dot{x} + R\dot{\psi}\cos\theta)\,\vec{\imath}_1 +
+(\dot{y} + R\dot{\psi}\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1
+\Longrightarrow
+\left\{
+\begin{array}{l}
+\dot{x} + R\dot{\psi}\cos\theta=0\\
+\dot{y} + R\dot{\psi}\,\mathrm{sen}\,\theta=0
+\end{array}
+\right.
+</math>
+</center>
+Estas ligaduras no se pueden integrar. Por ejemplo, la primera puede manipularse así
+<center>
+<math>
+\dfrac{\mathrm{d}x}{\mathrm{d}t} = -R\cos\theta\dfrac{\mathrm{d}\psi}{\mathrm{d}t}
+\Longrightarrow
+\int\mathrm{d}x = R\int\cos\theta\,\mathrm{d}\psi.
+</math>
+</center>
+La segunda integral no se puede hacer, pues <math>\theta</math> no es constante durante el movimiento y no sabemos como depende de <math>\psi</math>. Este es un caso en el que hay que describir el sistema con cuatro coordenadas generalizadas, <math>\{x, y,
+\theta, \psi\}</math>, aunque haya sólo dos grados de libertad.
+Veremos mas adelante
+que hay técnicas para tratar este tipo de problemas.

Introducción a la mecánica analítica (MR)

De Laplace

Revisión de 18:08 29 may 2018

Contenido

1 Introducción

2 Coordenadas generalizadas

2.1 Partícula puntual

2.2 Sistemas de partículas: Sólido Rígido

3 Ligaduras

3.1 Ligaduras holónomas

3.2 Ligaduras no holónomas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES