Primera Convocatoria 2017/18 (MR G.I.C.)
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Equilibrio de armadura con muelle== right En el sistema de la figura las barras tiene…') |
(→Equilibrio de armadura con muelle) |
||
| Línea 9: | Línea 9: | ||
#Calcula la energía potencial del sistema. | #Calcula la energía potencial del sistema. | ||
#Suponiendo que el muelle se ajusta de modo que <math>mg=kd</math>, determina los valores de <math>\theta</math> para los que hay equilibrio mecánico. Discute la estabilidad de estas posiciones de equilibrio. | #Suponiendo que el muelle se ajusta de modo que <math>mg=kd</math>, determina los valores de <math>\theta</math> para los que hay equilibrio mecánico. Discute la estabilidad de estas posiciones de equilibrio. | ||
| - | #Si se aplica una fuerza <math>\vec{F} = F_0\,\vec{\ | + | #Si se aplica una fuerza <math>\vec{F} = F_0\,\vec{\jmath}_1</math> sobre el punto <math>B</math>, con <math>F_0=2kd>0</math>, determina el nuevo valor de <math>\theta</math> para que haya equilibrio mecánico. |
última version al 20:10 11 feb 2018
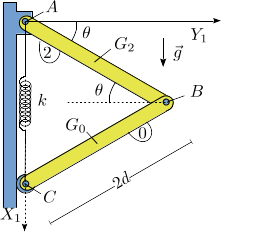
Equilibrio de armadura con muelle
En el sistema de la figura las barras tienen longitud 2d y masa m cada una. La barra "2" está articulada en el punto fijo A, mientras que el extremo C de la barra "0" puede deslizar sin rozamiento sobre la superficie vertical. El muelle que conecta los puntos A y C tiene constante elástica k y longitud natural nula. El muelle se mantiene siempre vertical. La gravedad actúa como se indica en la figura.
- Calcula la energía potencial del sistema.
- Suponiendo que el muelle se ajusta de modo que mg = kd, determina los valores de θ para los que hay equilibrio mecánico. Discute la estabilidad de estas posiciones de equilibrio.
- Si se aplica una fuerza
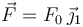sobre el punto B, con F0 = 2kd > 0, determina el nuevo valor de θ para que haya equilibrio mecánico.
