Los gases ideales (GIE)
De Laplace
| Línea 1: | Línea 1: | ||
| - | === | + | ==Introducción== |
| - | + | ==Presión y temperatura de un gas== | |
| + | El estado de un gas se caracteriza usualmente por dos variables independientes: su presión y su temperatura. De estas dos magnitudes se puede dar una visión puramente macroscópica, pero también se pueden interpretar en términos del modelo de gas ideal como formado por partículas puntuales no interactuantes. | ||
| - | + | ===Presión=== | |
| + | Supongamos que tenemos un cilindro lleno de un gas y que la tapa de este cilindro es un pistón que puede deslizarse sin rozamiento. Supongamos también que en el exterior del cilindro existe el vacío absoluto. En ese caso sabemos lo que ocurrirá: el gas del interior del cilindro se expandirá, desplazando al pistón (de forma más o menos acelerada, según la masa del pistón). | ||
| - | + | [[Archivo:presion-gas.jpg|right]] | |
| - | + | El mecanismo por el que esto ocurre son las colisiones de las moléculas de gas con el pistón. En cada colisión, supuesta elástica, la partícula experimenta un cambio en su cantidad de movimiento, que es ganado por el pistón. | |
| - | + | Por tanto, para mantener el pistón en su lugar, es preciso ejercer una fuerza externa sobre él en la dirección normal a su movimiento. La fuerza necesaria será mayor cuanto mayor sea el área del pistón, por lo que la fuerza externa que hay que aplicar es de la forma | |
| - | <center><math>\ | + | <center><math>F_\mathrm{ext} = p_\mathrm{ext}\,S\qquad\Rightarrow\qquad p_\mathrm{ext}=\frac{F_\mathrm{ext}}{S}</math></center> |
| - | siendo <math> | + | siendo <math>p_\mathrm{ext}</math> la fuerza aplicada por unidad de superficie. A esta cantidad se la denomina ''presión''. |
| - | + | Si conseguimos que el pistón se quede en equilibrio, llegamos a la conclusión de que la fuerza por unidad de superficie ejercida por el gas es igual a la aplicada desde fuera y por tanto el gas posee una presión | |
| - | + | ||
| - | = | + | <center><math>p = \frac{|F_\mathrm{ext}|}{S}</math></center> |
| - | + | ||
| - | + | Hemos definido la presión en términos de la fuerza aplicada desde fuera porque ésta es la que medimos fácilmente, si bien en estados de equilibrio, que son los que nos interesarán principalmente, podremos hablar igualmente de la fuerza aplicada desde el interior. | |
| - | + | La presión de un gas no es una magnitud dependiente de la superficie del gas, aunque sea ahí donde se mida. Es una propiedad de todo el gas. En una muestra de gas de tamaño reducido, todo el gas se encuentra a la misma presión y cualquier aumento en la presión en un punto se transmite a todos los puntos de la muestra (''principio de Pascal''). | |
| - | + | En una muestra de gas de gran tamaño la presión podrá variar de un punto a otro, incluso estando en equilibrio. Así, si tenemos un gas de densidad <math>\rho</math> homogénea sometido a la acción de la gravedad, la presión aumenta a medida que vamos bajando debido al peso de la columna de gas situada encima, siendo su variación | |
| - | <center><math> | + | <center><math>p(z) = p_0-\rho g z\,</math></center> |
| - | siendo <math> | + | siendo <math>p_0</math> la presión en el nivel que tomamos como referencia <math>z=0</math>. Dado que la densidad de un gas suele ser muy baja, este efecto es despreciable en la mayoría de las ocasiones, salvo que consideremos volúmenes de gas a escala atmosférica. |
| - | + | El segundo término, conocido como presión ''hidrostática'' sí es importante si además del gas tenemos una columna de líquido, como en el termómetro de gas a volumen constante. | |
| - | + | De la definición de presión se deduce que se mide en el SI en N/m². A esta unidad se la denomina pascal (Pa) | |
| - | <center><math>\frac{ | + | <center><math>1\,Pa = \frac{1\,\mathrm{N}}{1\,\mathrm{m}^2}</math></center> |
| - | + | Un pascal es una unidad muy pequeña, por lo que se suelen usar múltiplos. Así, un ''bar'' equivale a | |
| - | <center><math> | + | <center><math>1\,\mathrm{bar}= 100\,000\,\mathrm{Pa}</math></center> |
| - | + | y un milibar será | |
| - | <center><math> | + | <center><math>1\,\mathrm{mbar}= 0.001\,\mathrm{bar}=100\,\mathrm{Pa}</math></center> |
| - | + | Tres unidades que no pertenecen al SI son también de uso común al medir la presión: la atmósfera estándar | |
| - | + | ||
| - | <center><math>\ | + | <center><math>1\,\mathrm{atm}=101\,325\,\mathrm{Pa} \simeq 1013\,\mathrm{mbar}</math></center> |
| - | + | el milímetro de mercurio o torr | |
| - | <center><math> | + | <center><math>1\,\mathrm{Torr} = \frac{1\,\mathrm{atm}}{760}= 133.322\,\mathrm{Pa}</math></center> |
| - | + | y el psi (libra por pulgada cuadrada), habitual en la maquinaria anglosajona | |
| - | <center><math> | + | <center><math>1\,\mathrm{psi}=6895\,\mathrm{Pa}</math></center> |
| - | que | + | [[Archivo:manometro.jpg|300px|right]]A la hora de medir la presión, hay dos conceptos que conviene no confundir. |
| - | + | ;Presión absoluta: es la que se mide respecto a una presión nula, <math>p</math> | |
| + | ;Presión manométrica: es la que se mide respecto a la presión atmosférica | ||
| - | + | <center><math>p_\mathrm{manom.} = p - p_\mathrm{atm}</math></center> | |
| - | + | :La razón de la distinción es que la presión de un gas, como el que llena un neumático, se mide con un ''manómetro'', que se basa en la fuerza debida a la diferencia de presiones entre la presión del gas y la exterior, que suele ser la atmosférica. Por ello, al llenar un neumático con una presión de “2.1” hay que saber primero que la unidad es el bar (que es casi una atmósfera estándar) y segundo que la presión es manométrica, por lo que la verdadera presión del aire del neumático sería 3.1 bares. | |
| - | + | La diferencia entre manómetro y barómetro es que este último se usa para medir presiones atmosféricas, por lo que ya viene graduado en presiones absolutas (aunque internamente funcione como cualquier otro manómetro). | |
| - | + | ==Ecuación de estado== | |
| + | ===Ley de Boyle=== | ||
| + | La ley de Boyle (también conocida como ley de Boyle y Mariotte), nos dice que si en un gas ideal se mantiene la temperatura constante, la presión del gas es inversamente proporcional al volumen que ocupa, lo que se expresa | ||
| + | |||
| + | <center><math>T_1 = T_2\qquad\Rightarrow\qquad \frac{p_2}{p_1}=\frac{V_1}{V_2}\qquad \mbox{o}\qquad p_1V_1 = p_2V_2=f(T)</math></center> | ||
| + | |||
| + | Si aquí introducimos magnitudes específicas, dividiendo por la masa de gas, nos queda | ||
| + | |||
| + | <center><math>\frac{p_1}{\rho_1} = \frac{p_2}{\rho_2}</math></center> | ||
| + | |||
| + | o, equivalentemente, que la densidad de un gas ideal es proporcional a su presión, a temperatura constante | ||
| + | |||
| + | <center><math>p = f(T)\rho\qquad\qquad pV = F(T)</math></center> | ||
| + | |||
| + | con <math>F(T)</math> una cierta función de la temperatura y proporcional a la masa de gas. | ||
| + | |||
| + | <center>[[Archivo:Ley de Boyle.gif]]</center> | ||
| + | |||
| + | ===Ley de Charles=== | ||
| + | La ley de Charles (también llamada de Gay-Lussac, de Charles y Gay-Lussac, o de los volúmenes) afirma que en un gas ideal a presión constante, el volumen que ocupa el gas varía linealmente con la temperatura que tiene | ||
| + | |||
| + | <center><math>p_1=p_2\qquad\Rightarrow\qquad V(t) = A + B t</math></center> | ||
| + | |||
| + | o equivalentemente, que la temperatura de un gas ideal varía linealmente con el volumen que ocupa | ||
| + | |||
| + | <center><math>t = t_0+k V</math></center> | ||
| + | |||
| + | Experimentalmente se encuentra que la ordenada <math>t_0</math>, que representaría la temperatura a la cual el gas ideal ocuparía un volumen nulo (aunque ningún gas se puede llevar hasta esa temperatura), es independiente de la presión del gas siempre que sea baja y vale aproximadamente <math>t_0=-273.15^\circ\mathrm{C}</math>. Definiendo entonces la temperatura absoluta del gas como | ||
| + | |||
| + | <center><math>T = t - t_0 = t+273.15\,^\circ\mathrm{C}</math></center> | ||
| + | |||
| + | la ley de Charles se escribe | ||
| + | |||
| + | <center><math>T = kV\qquad\qquad\frac{V_2}{V_1}=\frac{T_2}{T_1}\qquad (p_1=p_2)</math></center> | ||
| + | |||
| + | <center>[[Archivo:Ley-de-charles.gif]]</center> | ||
| + | |||
| + | ===Ecuación general=== | ||
| + | Combinando la ley de Charles con la de Boyle obtenemos | ||
| + | |||
| + | <center><math>\left\{\begin{array}{ccc}T_1=T_2&\ & p_1V_1=p_2V_2 \\ && \\ p_1=p_2 & \ & \displaystyle\frac{V_1}{T_1}=\displaystyle \frac{V_2}{T_2}\end{array}\right\}\qquad\Rightarrow\qquad \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}</math></center> | ||
| + | |||
| + | o, equivalentemente, | ||
| + | |||
| + | <center><math>\frac{pV}{T}=K</math></center> | ||
| + | |||
| + | siendo K una constante específica para cada muestra de gas y que no depende ni de la presión, ni del volumen, ni de la temperatura. Puesto que el miembro es una cantidad extensiva (el volumen es proporcional a la masa), el segundo miembro también debe serlo, por lo que puede escribirse en la forma | ||
| + | |||
| + | <center><math>\frac{pV}{T}=MR_m</math></center> | ||
| + | |||
| + | siendo <math>R_m</math> una constante diferente para cada gas. | ||
| + | |||
| + | Se encuentra experimentalmente que si en lugar de emplear la masa usamos el número de moles, esta ecuación queda | ||
| + | |||
| + | <center><math>\frac{pV}{T}=nR</math></center> | ||
| + | |||
| + | siendo <math>R</math> una constante que no depende del gas del que se trate. A esta cantidad se la denomina constante de los gases ideales y su valor en el SI es | ||
| + | |||
| + | <center><math>R = 8.314\,4621(75)\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\simeq 8.31\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}</math></center> | ||
| + | |||
| + | Esta ecuación de estado suele escribirse en la forma | ||
| + | |||
| + | <center><math>pV = nRT\,</math></center> | ||
| - | + | ===Aplicaciones. Termómetro a volumen constante=== | |
| - | + | ==Gases no ideales. Compresibilidad== | |
| + | ==Trabajo, calor y energía== | ||
| + | Como todo sistema termodinámico, sobre un gas se puede realizar trabajo e introducir calor, variando su energía interna | ||
| + | ===Trabajo=== | ||
| + | El trabajo sobre un gas se realiza variando el volumen que ocupa. Consideremos un cilindro con un pistón de área <math>S</math>. Cuando sobre este pistón se ejerce una fuerza normal <math>F</math> el pistón se desplaza una cantidad <math>\mathrm{d}x</math>. En este proceso se realiza un trabajo diferencial | ||
| - | <center><math> | + | <center><math>\mathrm{d}W=F\,(-\mathrm{d}x) = \left(\frac{F}{S}\right)\,(-\mathrm{S}\,\mathrm{d}x)</math></center> |
| - | + | El signo negativo en <math>-\mathrm{d}x</math> se debe a que el trabajo realizado sobre el gas es positivo cuando el gas se comprime y el émbolo se desplaza hacia el interior del gas. En la última ecuación el primer factor es la presión ejercida sobre el émbolo, mientras que el segundo es la disminución de volumen del gas. Por tanto, el trabajo diferencial es igual a | |
| - | <center><math> | + | <center><math>\mathrm{d}W=-p\,\mathrm{d}V</math></center> |
| - | + | Hay que destacar que en esta expresión <math>p</math> es la presión exterior, no la propia del gas. Sólo en procesos cuasiestáticos en que la presión interior iguala prácticamente a la exterior, se podrá sustituir una por otra. | |
| - | + | ===Energía interna=== | |
| + | En principio, la energía interna de un gas puede depender de su temperatura y de su volumen (por ser dos variables independientes). Sin embargo, Joule descubrió que para un gas aproximadamente ideal, la energía interna no depende del volumen, sino solo de su temperatura. | ||
| - | + | <center><math>U=U(T)\,</math></center> | |
| - | + | La experiencia de Joule consistió en medir la temperatura de un gas, someterlo a una expansión brusca en el vacío rompiendo un diafragma, y volver a medir la temperatura. Por no haber presión exterior el trabajo es nulo. Por ser una expansión brusca el proceso es prácticamente adiabático y no hay calor transferido al sistema. Por tanto, la energía interna del gas permanece constante | |
| - | + | <center><math>\Delta U = W + Q = 0\,</math></center> | |
| - | + | Cuando midió la temperatura final, Joule obtuvo que su valor era prácticamente igual a la inicial. Puesto que la temperatura no cambia, pero el volumen sí, y resulta que la energía interna permanece constante, se llega a la conclusión de que U no depende del volumen y sólo es función de la temperatura. | |
| + | ===Procesos en un gas ideal=== | ||
| + | ====Isócoros==== | ||
| + | ====Isóbaros==== | ||
| + | ====Isotermos==== | ||
| + | ====Adiabáticos==== | ||
| - | de | + | ==Coeficientes termodinámicos== |
| + | ==Entropía de un gas ideal== | ||
| + | [[Categoría:Física II (GIE)]] | ||
Revisión de 17:26 7 feb 2018
Contenido |
1 Introducción
2 Presión y temperatura de un gas
El estado de un gas se caracteriza usualmente por dos variables independientes: su presión y su temperatura. De estas dos magnitudes se puede dar una visión puramente macroscópica, pero también se pueden interpretar en términos del modelo de gas ideal como formado por partículas puntuales no interactuantes.
2.1 Presión
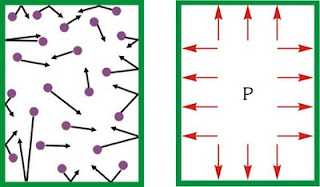
Supongamos que tenemos un cilindro lleno de un gas y que la tapa de este cilindro es un pistón que puede deslizarse sin rozamiento. Supongamos también que en el exterior del cilindro existe el vacío absoluto. En ese caso sabemos lo que ocurrirá: el gas del interior del cilindro se expandirá, desplazando al pistón (de forma más o menos acelerada, según la masa del pistón).
El mecanismo por el que esto ocurre son las colisiones de las moléculas de gas con el pistón. En cada colisión, supuesta elástica, la partícula experimenta un cambio en su cantidad de movimiento, que es ganado por el pistón.
Por tanto, para mantener el pistón en su lugar, es preciso ejercer una fuerza externa sobre él en la dirección normal a su movimiento. La fuerza necesaria será mayor cuanto mayor sea el área del pistón, por lo que la fuerza externa que hay que aplicar es de la forma
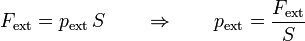
siendo pext la fuerza aplicada por unidad de superficie. A esta cantidad se la denomina presión.
Si conseguimos que el pistón se quede en equilibrio, llegamos a la conclusión de que la fuerza por unidad de superficie ejercida por el gas es igual a la aplicada desde fuera y por tanto el gas posee una presión
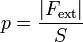
Hemos definido la presión en términos de la fuerza aplicada desde fuera porque ésta es la que medimos fácilmente, si bien en estados de equilibrio, que son los que nos interesarán principalmente, podremos hablar igualmente de la fuerza aplicada desde el interior.
La presión de un gas no es una magnitud dependiente de la superficie del gas, aunque sea ahí donde se mida. Es una propiedad de todo el gas. En una muestra de gas de tamaño reducido, todo el gas se encuentra a la misma presión y cualquier aumento en la presión en un punto se transmite a todos los puntos de la muestra (principio de Pascal).
En una muestra de gas de gran tamaño la presión podrá variar de un punto a otro, incluso estando en equilibrio. Así, si tenemos un gas de densidad ρ homogénea sometido a la acción de la gravedad, la presión aumenta a medida que vamos bajando debido al peso de la columna de gas situada encima, siendo su variación
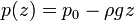
siendo p0 la presión en el nivel que tomamos como referencia z = 0. Dado que la densidad de un gas suele ser muy baja, este efecto es despreciable en la mayoría de las ocasiones, salvo que consideremos volúmenes de gas a escala atmosférica.
El segundo término, conocido como presión hidrostática sí es importante si además del gas tenemos una columna de líquido, como en el termómetro de gas a volumen constante.
De la definición de presión se deduce que se mide en el SI en N/m². A esta unidad se la denomina pascal (Pa)
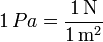
Un pascal es una unidad muy pequeña, por lo que se suelen usar múltiplos. Así, un bar equivale a
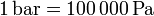
y un milibar será
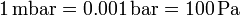
Tres unidades que no pertenecen al SI son también de uso común al medir la presión: la atmósfera estándar
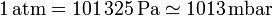
el milímetro de mercurio o torr
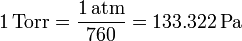
y el psi (libra por pulgada cuadrada), habitual en la maquinaria anglosajona
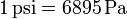
- Presión absoluta
- es la que se mide respecto a una presión nula, p
- Presión manométrica
- es la que se mide respecto a la presión atmosférica
- La razón de la distinción es que la presión de un gas, como el que llena un neumático, se mide con un manómetro, que se basa en la fuerza debida a la diferencia de presiones entre la presión del gas y la exterior, que suele ser la atmosférica. Por ello, al llenar un neumático con una presión de “2.1” hay que saber primero que la unidad es el bar (que es casi una atmósfera estándar) y segundo que la presión es manométrica, por lo que la verdadera presión del aire del neumático sería 3.1 bares.
La diferencia entre manómetro y barómetro es que este último se usa para medir presiones atmosféricas, por lo que ya viene graduado en presiones absolutas (aunque internamente funcione como cualquier otro manómetro).
3 Ecuación de estado
3.1 Ley de Boyle
La ley de Boyle (también conocida como ley de Boyle y Mariotte), nos dice que si en un gas ideal se mantiene la temperatura constante, la presión del gas es inversamente proporcional al volumen que ocupa, lo que se expresa
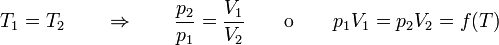
Si aquí introducimos magnitudes específicas, dividiendo por la masa de gas, nos queda
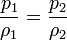
o, equivalentemente, que la densidad de un gas ideal es proporcional a su presión, a temperatura constante

con F(T) una cierta función de la temperatura y proporcional a la masa de gas.
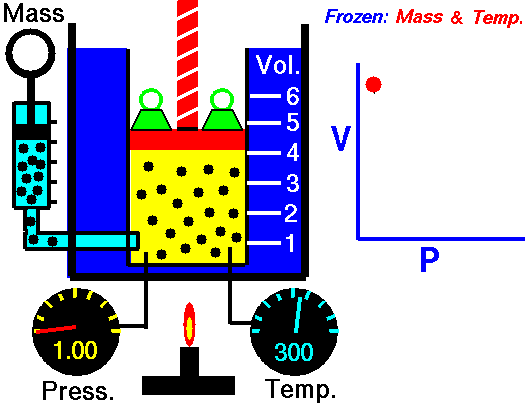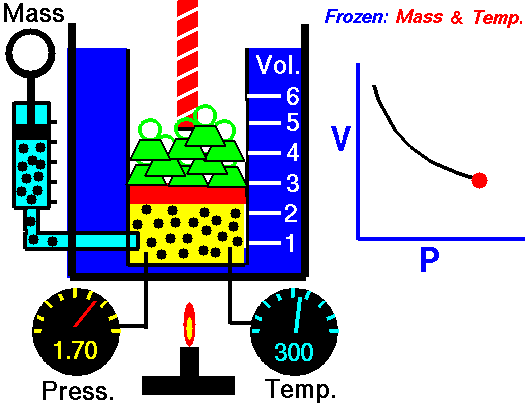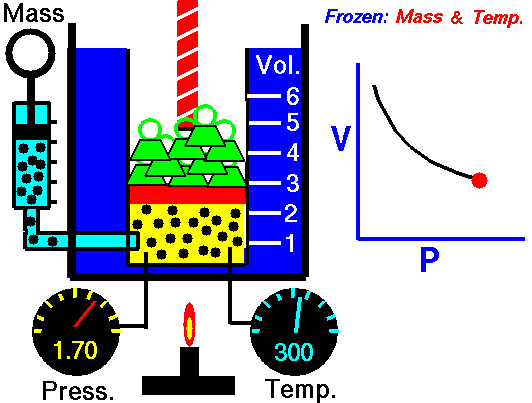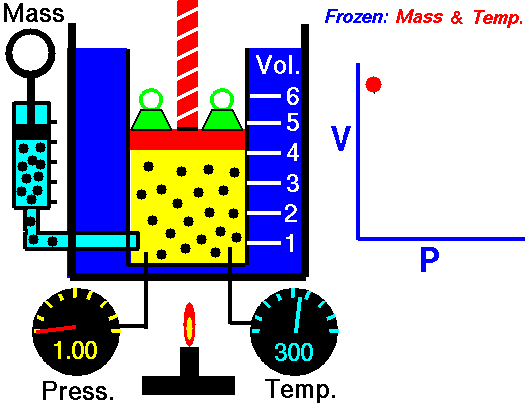
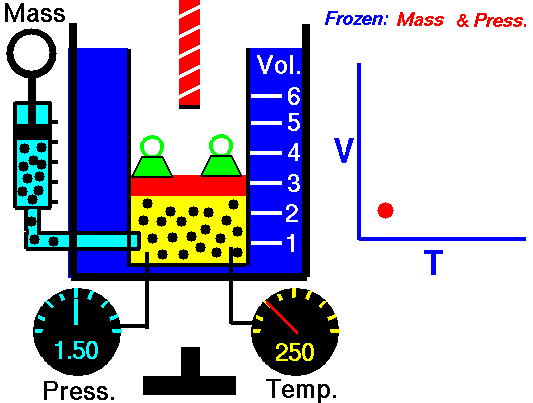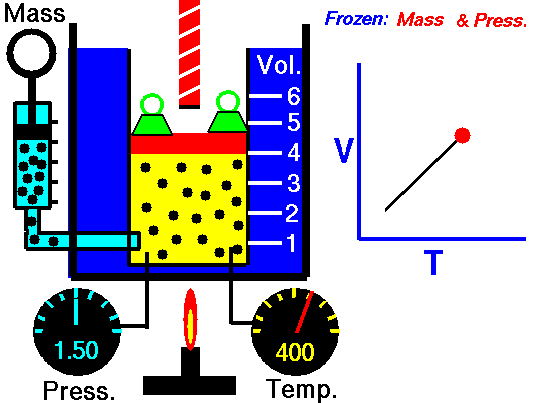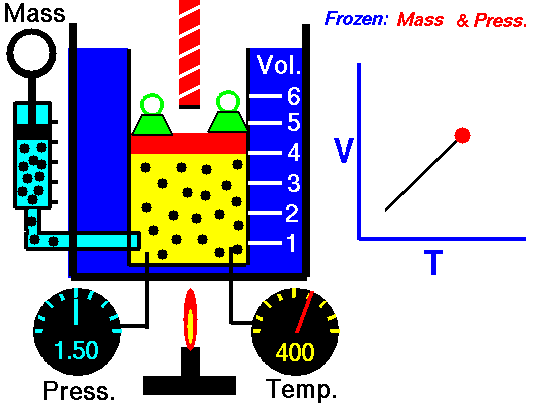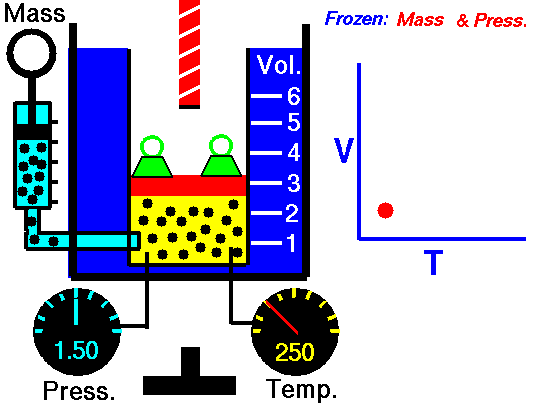
3.2 Ley de Charles
La ley de Charles (también llamada de Gay-Lussac, de Charles y Gay-Lussac, o de los volúmenes) afirma que en un gas ideal a presión constante, el volumen que ocupa el gas varía linealmente con la temperatura que tiene

o equivalentemente, que la temperatura de un gas ideal varía linealmente con el volumen que ocupa
Experimentalmente se encuentra que la ordenada t0, que representaría la temperatura a la cual el gas ideal ocuparía un volumen nulo (aunque ningún gas se puede llevar hasta esa temperatura), es independiente de la presión del gas siempre que sea baja y vale aproximadamente 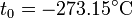 . Definiendo entonces la temperatura absoluta del gas como
. Definiendo entonces la temperatura absoluta del gas como

la ley de Charles se escribe
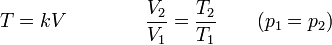
3.3 Ecuación general
Combinando la ley de Charles con la de Boyle obtenemos
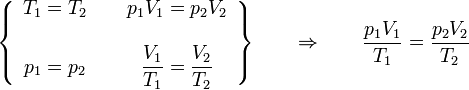
o, equivalentemente,
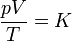
siendo K una constante específica para cada muestra de gas y que no depende ni de la presión, ni del volumen, ni de la temperatura. Puesto que el miembro es una cantidad extensiva (el volumen es proporcional a la masa), el segundo miembro también debe serlo, por lo que puede escribirse en la forma
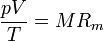
siendo Rm una constante diferente para cada gas.
Se encuentra experimentalmente que si en lugar de emplear la masa usamos el número de moles, esta ecuación queda
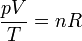
siendo R una constante que no depende del gas del que se trate. A esta cantidad se la denomina constante de los gases ideales y su valor en el SI es

Esta ecuación de estado suele escribirse en la forma
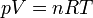
3.4 Aplicaciones. Termómetro a volumen constante
4 Gases no ideales. Compresibilidad
5 Trabajo, calor y energía
Como todo sistema termodinámico, sobre un gas se puede realizar trabajo e introducir calor, variando su energía interna
5.1 Trabajo
El trabajo sobre un gas se realiza variando el volumen que ocupa. Consideremos un cilindro con un pistón de área S. Cuando sobre este pistón se ejerce una fuerza normal F el pistón se desplaza una cantidad dx. En este proceso se realiza un trabajo diferencial
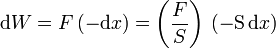
El signo negativo en − dx se debe a que el trabajo realizado sobre el gas es positivo cuando el gas se comprime y el émbolo se desplaza hacia el interior del gas. En la última ecuación el primer factor es la presión ejercida sobre el émbolo, mientras que el segundo es la disminución de volumen del gas. Por tanto, el trabajo diferencial es igual a
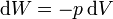
Hay que destacar que en esta expresión p es la presión exterior, no la propia del gas. Sólo en procesos cuasiestáticos en que la presión interior iguala prácticamente a la exterior, se podrá sustituir una por otra.
5.2 Energía interna
En principio, la energía interna de un gas puede depender de su temperatura y de su volumen (por ser dos variables independientes). Sin embargo, Joule descubrió que para un gas aproximadamente ideal, la energía interna no depende del volumen, sino solo de su temperatura.
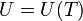
La experiencia de Joule consistió en medir la temperatura de un gas, someterlo a una expansión brusca en el vacío rompiendo un diafragma, y volver a medir la temperatura. Por no haber presión exterior el trabajo es nulo. Por ser una expansión brusca el proceso es prácticamente adiabático y no hay calor transferido al sistema. Por tanto, la energía interna del gas permanece constante
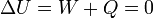
Cuando midió la temperatura final, Joule obtuvo que su valor era prácticamente igual a la inicial. Puesto que la temperatura no cambia, pero el volumen sí, y resulta que la energía interna permanece constante, se llega a la conclusión de que U no depende del volumen y sólo es función de la temperatura.