Movimiento circular alrededor de un eje (GIE)
De Laplace
(Diferencias entre revisiones)
(→Centro de curvatura) |
(→Centro de curvatura) |
||
| Línea 26: | Línea 26: | ||
<center><math>\vec{N}=\frac{\vec{a}_n}{a_n}=-\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}</math></center> | <center><math>\vec{N}=\frac{\vec{a}_n}{a_n}=-\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}</math></center> | ||
y | y | ||
| - | <center><math>\vec{r}_c=\vec{r}+R\vec{N}=(14\vec{\imath}-5\vec{\jmath}-2\vec{k})+12\left(-\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}\right)=6\vec{\imath}+3\vec{\jmath}-6\vec{k}</math></center> | + | <center><math>\vec{r}_c=\vec{r}+R\vec{N}=(14\vec{\imath}-5\vec{\jmath}-2\vec{k})+12\left(-\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}\right)=(6\vec{\imath}+3\vec{\jmath}-6\vec{k})\,\mathrm{m}</math></center> |
==Distancia recorrida== | ==Distancia recorrida== | ||
última version al 21:10 31 ene 2018
Contenido |
1 Enunciado
Una partícula describe un movimiento circular uniforme alrededor de un eje que pasa por el origen de coordenadas, siendo la velocidad angular constante 
(rad/s). La posición inicial de la partícula es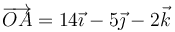 
(m). Para este movimiento, halle:
- La velocidad inicial de la partícula, así como la rapidez en dicho instante.
- La aceleración inicial de la partícula.
- Las componentes intrínsecas de la aceleración (escalares) en ese instante.
- El radio y el centro de curvatura del movimiento.
- La distancia recorrida por la partícula entre t = 0 s y t = 10 s
2 Velocidad y rapidez
2.1 Velocidad
2.2 Rapidez
3 Aceleración
4 Componentes intrínsecas
4.1 Aceleración tangencial
Por ser uniforme, at = 0
4.2 Aceleración normal
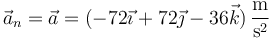
y
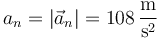
5 Radio y centro de curvatura
5.1 Radio de curvatura
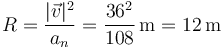
5.2 Centro de curvatura
y
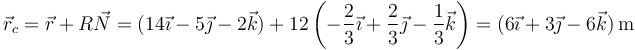
6 Distancia recorrida
Por ser uniforme
