Estudio analítico de una barra apoyada
De Laplace
(Diferencias entre revisiones)
(Página creada con 'Como en el problema “Barra deslizante con masas en los extremos”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vert…') |
|||
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
Como en el problema “[[Barra deslizante con masas en los extremos]]”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies | Como en el problema “[[Barra deslizante con masas en los extremos]]”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies | ||
Revisión de 17:11 20 ene 2018
Contenido |
1 Enunciado
Como en el problema “Barra deslizante con masas en los extremos”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies
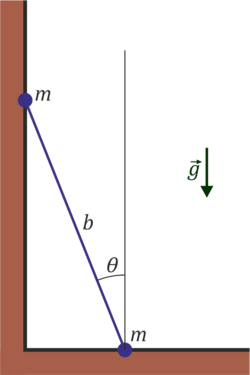
- Determine la lagrangiana del sistema.
- Halle la ecuación de movimiento para el ángulo θ.
- Determine una constante de movimiento no trivial.
- Añadiendo una coordenada x que representaría la separación de la barra respecto de la pared vertical, calcule la fuerza de reacción ejercida por la pared.
- Existe un valor de θ para el cual la barra se separa de la pared. Determine este valor.
- Halle la ecuación de movimiento para la barra una vez que se ha separado de la pared.





