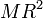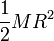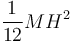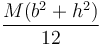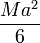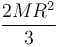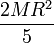Momento y tensor de inercia (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 23:02 13 ene 2018

Contenido

1 Introducción
2 Tensor de inercia
3 Momento de inercia
4 Teorema de Steiner y de la figura plana
- 4.1 Teorema de Steiner o de los ejes paralelos
- 4.2 Teorema de la figura plana o de los ejes perpendiculares
5 Producto de inercia
6 El tensor de inercia
7 Producto diádico y tensor de inercia
8 Ejes principales y momentos principales de inercia
9 Rotación de ejes

1 Introducción

El momento de inercia de un sistema de partículas respecto a un punto A puede definirse de dos maneras: empleando velocidades absolutas respecto a un sistema de referencia inercial

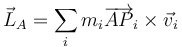
$\vec{L}_A=\sum_i m_i \overrightarrow{AP}_i\times\vec{v}_i$

o usando las velocidades relativas

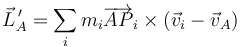
$\vec{L}^{\,\prime}_A=\sum_i m_i \overrightarrow{AP}_i\times(\vec{v}_i-\vec{v}_A)$

Ambas cantidades se relacionan por la igualdad

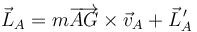
$\vec{L}_A=m\overrightarrow{AG}\times\vec{v}_A+\vec{L}^{\,\prime}_A$

con lo cual ambas expresiones son coincidentes en los casos importantes

A es un punto fijo.
A es el propio centro de masas.

En el caso particular de un sólido rígido tenemos una expresión simple para las velocidades relativas

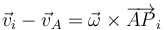
$\vec{v}_i-\vec{v}_A=\vec{\omega}\times\overrightarrow{AP}_i$

por lo que el momento cinético relativo queda, para un sólido

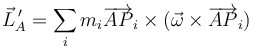
$\vec{L}^{\,\prime}_A=\sum_i m_i\overrightarrow{AP}_i\times(\vec{\omega}\times\overrightarrow{AP}_i)$

Esta cantidad es proporcional a la velocidad angular en el sentido de que a doble velocidad angular le corresponde doble momento cinético. Sin embargo, en general ambos vectores no son paralelos, por lo que la relación no se reduce a multiplicar la velocidad angular por un número. En su lugar, la proporcionalidad se establece mediante un tensor, el cual se puede representar por una matriz, de manera que la relación entre las componentes del momento cinético y de la velocidad angular se puede escribir en la forma

$\begin{pmatrix}L'_{Ax}\\ L'_{Ay}\\ L'_{Az}\end{pmatrix}=\begin{pmatrix}I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix}\cdot\begin{pmatrix}\omega_{x}\\ \omega_{y}\\ \omega_{z}\end{pmatrix}$

o, en forma simbólica,

$\vec{L}^{\,\prime}_A=\bar{\bar{I}}\cdot\vec{\omega}$

Esta cantidad matricial se denomina el tensor de inercia. En lo que sigue veremos sus principales propiedades y casos particulares.

2 Tensor de inercia

Para obtener las componentes del tensor de inercia a partir del momento cinético, consideramos las componentes cartesianas de los vectores

$\vec{\omega}=\omega_x\vec{\imath}+\omega_y\vec{\jmath}+\omega_z\vec{k}\qquad\qquad \overrightarrow{AP}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$

y aplicamos que

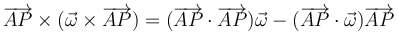
$\overrightarrow{AP}\times(\vec{\omega}\times\overrightarrow{AP})=(\overrightarrow{AP}\cdot\overrightarrow{AP})\vec{\omega}-(\overrightarrow{AP}\cdot\vec{\omega})\overrightarrow{AP}$

Esto nos da, para la componente x del momento cinético

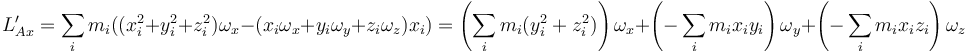
$L'_{Ax}=\sum_i m_i((x_i^2+y_i^2+z_i^2)\omega_x-(x_i\omega_x+y_i\omega_y+z_i\omega_z)x_i)= \left(\sum_i m_i(y_i^2+z_i^2)\right)\omega_x +\left(-\sum_im_ix_iy_i\right)\omega_y+\left(-\sum_im_ix_iz_i\right)\omega_z$

Por otro lado, si desarrollamos la expresión matricial anterior queda, para la componente x

L' A x = I x x ω x + I x y ω y + I x z ω z

lo que nos permite identificar las componentes buscadas, como los coeficientes de las componentes de la velocidad angular:

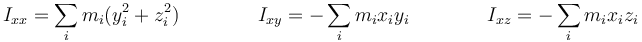
$I_{xx}=\sum_i m_i(y_i^2+z_i^2)\qquad\qquad I_{xy}=-\sum_im_ix_iy_i\qquad\qquad I_{xz}= -\sum_im_ix_iz_i$

y análogamente para las otras dos filas

$I_{yx}=-\sum_im_ix_iy_i\qquad\qquad I_{yy}=\sum_i m_i(x_i^2+z_i^2)\qquad\qquad I_{yz}= -\sum_im_iy_iz_i$

y

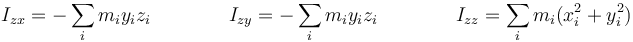
$I_{zx}=-\sum_im_iy_iz_i\qquad\qquad I_{zy}=-\sum_im_iy_iz_i\qquad\qquad I_{zz} = \sum_i m_i(x_i^2+y_i^2)$

3 Momento de inercia

3.1 Respecto a un eje

Dado un sólido rígido, se define su momento de inercia respecto a un eje como la cantidad

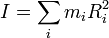
$I = \sum_i m_i R_i^2\,$

donde $R i$ es la distancia de una partícula $m 1$ al eje. En el caso de que tengamos una distribución continua, la expresión correspondiente es la integral

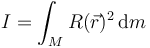
$I = \int_M R(\vec{r})^2\,\mathrm{d}m$

donde $R$ será en general diferente para cada elemento de masa $d m$ .

De la definición del momento de inercia se deduce que sus dimensiones son de una masa por una longitud al cuadrado y sus unidades en el SI son kg·m²

En los casos particulares frecuentes de que el eje respecto al que se calcula el momento de inercia se haga coincidir con uno de los ejes de coordenadas obtenemos los momentos de inercia

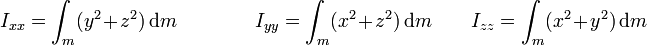
$I_{xx}=\int_m(y^2+z^2)\,\mathrm{d}m\qquad\qquad I_{yy}=\int_m(x^2+z^2)\,\mathrm{d}m\qquad I_{zz}=\int_m(x^2+y^2)\,\mathrm{d}m$

Rotor equilibrado

Consideremos un rotor formado por dos masas iguales de valor $m$ situadas en los extremos de una varilla rígida ideal (sin masa) de longitud $H$ con un eje de giro perpendicular a ella y que pasa por su centro. La distancia de cada masa al eje es la mitad de la longitud de la varilla, por lo que

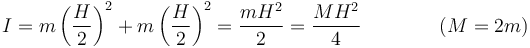
$I = m\left(\frac{H}{2}\right)^2 +m\left(\frac{H}{2}\right)^2 = \frac{mH^2}{2}=\frac{MH^2}{4}\qquad\qquad (M = 2m)$

Varilla homogénea

Una barra de longitud H con una masa M distribuida uniformemente posee un momento de inercia respecto a un eje perpendicular a ella por su centro

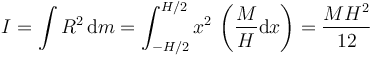
$I = \int R^2\,\mathrm{d}m=\int_{-H/2}^{H/2} x^2\,\left(\frac{M}{H}\mathrm{d}x\right)=\frac{MH^2}{12}$

Superficie cilíndrica

Para una superficie cilíndrica de radio $R$ y altura $h$ , el momento de inercia respecto al eje del cilindro es, simplemente

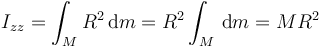
$I_{zz}=\int_M R^2\,\mathrm{d}m = R^2\int_M\,\mathrm{d}m = {MR^2}$

ya que todos los puntos se encuentran a la misma distancia del eje.

Puesto que este resultado no depende de la altura del cilindro también es aplicable al caso de un anillo (superficie cilíndrica de altura muy pequeña).

Cilindro macizo

Si en cambio consideramos un cilindro macizo homogéneo de radio $R$ y altura $h$ , su momento de inercia es igual a

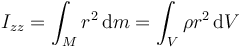
$I_{zz}=\int_M {r^2}\,\mathrm{d}m = \int_V \rho r^2\,\mathrm{d}V$

Como elementos de volumen consideramos finas películas cilíndricas de radio $r$ y espesor $d r$ , cada una de las cuales tiene el volumen diferencial

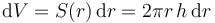
$\mathrm{d}V = {S(r)}\,\mathrm{d}r = 2\pi r\,h\,\mathrm{d}r$

Llevando esto al momento de inercia nos queda

$I_{zz} = \int_0^R \rho\,r^2\,(2\pi\,r\,h)\mathrm{d}r = 2\pi\rho h\int_0^R r^3\,\mathrm{d}r=\frac{\pi \rho R^4 h}{2}$

Vemos que para cilindros del mismo material (con la misma densidad de masa), el momento de inercia va como la cuarta potencia del radio (esto es, doble de radio significa que el momento de inercia se multiplica por 16). Sustituyendo el valor de la densidad de masa

$\rho = \frac{M}{V}=\frac{M}{\pi R^2 h}\qquad\Rightarrow\qquad I_{zz}=\frac{1}{2}{MR^2}$

El momento de inercia de un cilindro macizo es entonces la mitad del de una superficie cilíndrica de la misma masa y el mismo radio.

Puesto que este resultado no depende de la altura del cilindro también es aplicable al caso de un disco (cilindro macizo de muy pequeño espesor).

3.2 Casos particulares

Por su interés, es conveniente tabular casos particulares de momentos de inercia de sólidos homogéneos. Muchos otros pueden hallarse

Sólido	Eje	Momento de inercia
Superficie cilíndrica de radio $R$ y altura $h$	El del cilindro	$MR^2\,$
Cilindro macizo de radio $R$ y altura $h$	El del cilindro	$\frac{1}{2}MR^2$
Cilindro hueco de radio interior $R 1$ , exterior $R 2$ y altura $h$	El del cilindro	$\frac{1}{2}M\left(R_1^2+R_2^2\right)$
Varilla rectilínea de longitud $H$	Perpendicular por el centro	$\frac{1}{12}MH^2$
Paralelogramo de lados $b$ y $h$ (incluye cuadrados, rectángulos y rombos)	Perpendicular por el centro	$\frac{M(b^2+h^2)}{12}$
Cubo macizo de arista $a$	Cualquiera que pase por su centro	$\frac{Ma^2}{6}$
Superficie esférica de radio $R$	Cualquiera que pase por su centro	$\frac{2MR^2}{3}$
Esfera maciza de radio $R$	Cualquiera que pase por su centro	$\frac{2MR^2}{5}$

Vemos que para aquellos que se caracterizan por una sola distancia R (radio, longitud,...), la forma del momento de inercia es

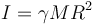
$I=\gamma M R^2\,$

con γ un número que depende del objeto. En particular, para objetos redondos (con R el radio) tenemos

Cuerpo	Cilindro hueco	Cilindro macizo	Esfera hueca	Esfera maciza
$\gamma\,$	$1\,$	$\frac{1}{2}$	$\frac{2}{3}$	$\frac{2}{5}$

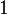
Esto permite estudiar de forma general los problemas de objetos rodantes, suponiendo un cierto factor γ general y luego particularizando.

3.3 Respecto a un plano

El concepto de momento de inercia se puede generalizar considerando otros tipos de distancias. Así, definimos el momento de inercia respecto a un plano como

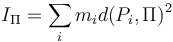
$I_\Pi = \sum_i m_i d(P_i,\Pi)^2\,$

Para el caso de los planos coordenados, esto da

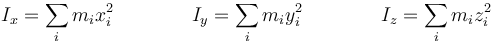
$I_x = \sum_i m_i x_i^2\qquad\qquad I_y = \sum_i m_i y_i^2 \qquad\qquad I_z = \sum_i m_i z_i^2$

De esta definición es inmediato que el momento de inercia respecto a un eje se puede poner como suma de los momentos respecto a dos planos ortogonales. Para los planos y ejes coordenados:

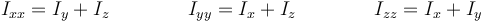
$I_{xx}=I_y+I_z \qquad\qquad I_{yy}=I_x+I_z \qquad\qquad I_{zz}=I_x+I_y$

Estas relaciones pueden invertirse para dar

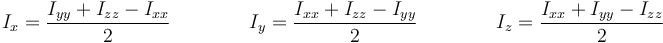
$I_x = \frac{I_{yy}+I_{zz}-I_{xx}}{2}\qquad\qquad I_y = \frac{I_{xx}+I_{zz}-I_{yy}}{2}\qquad\qquad I_z = \frac{I_{xx}+I_{yy}-I_{zz}}{2}$

3.4 Respecto a un punto

De la misma manera, puede definirse el momento de inercia respecto a un punto tomando las distancias a éste. Para el caso del origen de coordenadas

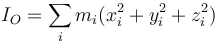
$I_O=\sum_i m_i(x_i^2+y_i^2+z_i^2)\,$

Este momento de inercia se relaciona con los momentos de inercia respecto al origen y a los planos coordenados como

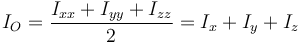
$I_O=\frac{I_{xx}+I_{yy}+I_{zz}}{2}=I_x+I_y+I_z$

Momento de inercia de una superficie esférica respecto a un diámetro

El momento de inercia respecto a un punto nos permite hallar de forma sencilla el momento de inercia de una esfera respecto a un eje que pasa por su centro. Supongamos una superficie esférica de masa M y radio R centrada en el origen. Por la simetría del sistema, debe ser

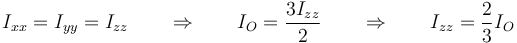
$I_{xx}=I_{yy}=I_{zz}\qquad\Rightarrow\qquad I_O=\frac{3I_{zz}}{2}\qquad\Rightarrow\qquad I_{zz}=\frac{2}{3}I_O$

Por otro lado, todos los puntos de la superficie se hallan a la misma distancia del origen, por lo que

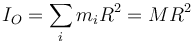
$I_O=\sum_i m_i R^2 = M R^2\,$

y por tanto

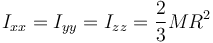
$I_{xx}=I_{yy}=I_{zz}=\frac{2}{3}MR^2$

Momento de inercia de una esfera maciza respecto a un diámetro

De la misma manera se halla el momento de inercia para una esfera maciza. Por la simetría tenemos

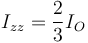
$I_{zz}=\frac{2}{3}I_O$

Pero ahora no todos los puntos se hallan a la misma distancia. Calculamos el momento de inercia respecto al centro descomponiendo la esfera en cáscaras esféricas de radio $r$ y espesor $d r$ . Para cada cáscara

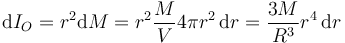
$\mathrm{d}I_O=r^2 \mathrm{d}M = r^2 \frac{M}{V} 4\pi r^2\,\mathrm{d}r=\frac{3M}{R^3}r^4\,\mathrm{d}r$

Integramos para toda la esfera

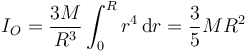
$I_O=\frac{3M}{R^3}\int_0^R r^4\,\mathrm{d}r= \frac{3}{5}MR^2$

y por tanto, para una esfera maciza

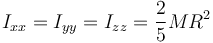
$I_{xx}=I_{yy}=I_{zz}=\frac{2}{5}MR^2$

4 Teorema de Steiner y de la figura plana

4.1 Teorema de Steiner o de los ejes paralelos

El momento de inercia puede definirse respecto a un eje arbitrario, que no necesariamente debe pasar por el centro de masas del sólido. No obstante, los ejes que pasan por el CM tienen propiedades particulares.

Consideremos dos ejes paralelos: uno que pasa por el CM y uno situado a una distancia $d$ del primero. Sea $I G$ el momento de inercia respecto al eje que pasa por el CM e $I$ el momento de inercia respecto al eje paralelo. Buscamos una relación entre estas dos cantidades.

Si consideramos el eje Z como el paralelo al que pasa por el CM el momento de inercia se puede escribir

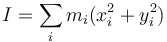
$I = \sum_i m_i(x_i^2+y_i^2)$

Introduciendo las posiciones relativas al CM

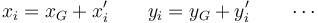
$x_i = x_G + x_i'\qquad y_i = y_G + y_i'\qquad \cdots$

queda

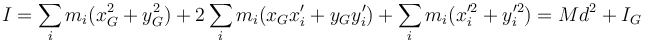
$I=\sum_i m_i(x_G^2+y_G^2) + 2\sum_i m_i(x_Gx'_i+y_Gy'_i)+\sum_i m_i(x_i^{\prime 2}+y_i^{\prime 2}) = M d^2+ I_G$

donde el término central se anula por ser nula la posición del CM respecto a sí mismo.

Este es el teorema de Steiner o de los ejes paralelos. Nos permite calcular el momento de inercia respecto a un eje arbitrario si conocemos el valor respecto a un eje paralelo que pase por el CM.

Este teorema nos dice que el momento de inercia en ejes paralelos es mínimo en el eje que pasa por el CM (lo cual sirve también como definición del centro de masas).

Varilla homogénea

Por ejemplo, consideremos el momento de inercia de una varilla de masa M y longitud H alrededor de un eje que pasa por su extremo.

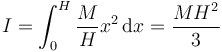
$I= \int_{0}^{H}\frac{M}{H}x^2\,\mathrm{d}x = \frac{MH^2}{3}$

Si hallamos la diferencia con el que calculamos antes para el eje que pasa por el centro

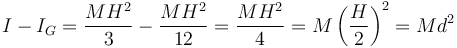
$I - I_G = \frac{MH^2}{3}-\frac{MH^2}{12}= \frac{MH^2}{4}=M\left(\frac{H}{2}\right)^2 = Md^2$

4.2 Teorema de la figura plana o de los ejes perpendiculares

Una sólido puede considerarse plano cuando sus dimensiones en una determinada dirección son mucho más pequeñas que a lo largo de las normales a ella. Es el caso, por ejemplo, de una chapa metálica en forma de disco o el de una varilla.

Si consideramos que la coordenada $z$ es la que tiene espesor despreciable, podemos suponer que $z = 0$ para todos los puntos del sólido. Esto implica que el momento de inercia respecto a este plano es nulo y por tanto

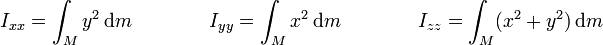
$I_{xx}=\int_M y^2\,\mathrm{d}m\qquad\qquad I_{yy}=\int_M x^2\,\mathrm{d}m \qquad\qquad I_{zz}=\int_M (x^2+y^2)\,\mathrm{d}m$

de donde es inmediato que

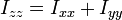
$I_{zz} = I_{xx}+I_{yy}\,$

Esta relación permite calcular uno de los momentos de inercia conocidos los otros dos.

Disco homogéneo

Por ejemplo, si deseamos hallar el momento de inercia de un disco circular respecto a un eje diametral podemos aplicar que, por simetría y por el teorema de la figura plana

$\left\{\begin{array}{rcl}I_{xx} &= & I_{yy} \\ && \\ I_{xx}+I_{yy} &= & I_{zz}=\displaystyle\frac{1}{2}MR^2\end{array}\right.\qquad\Rightarrow\qquad I_{xx}=I_{yy}=\frac{1}{4}{MR^2}$

5 Producto de inercia

Además de los momentos de inercia, se definen los productos de inercia como

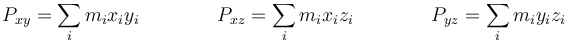
$P_{xy}=\sum_i m_i x_iy_i\qquad \qquad P_{xz}=\sum_i m_i x_i z_i \qquad\qquad P_{yz}=\sum_i m_i y_iz_i\,$

Estas cantidades son de interés porque aparecen en la expresión general del momento cinético de un sistema.

6 El tensor de inercia

Cuando se calcula el momento cinético de un sistema general, el término debido a la rotación es de la forma

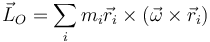
$\vec{L}_O=\sum_i m_i \vec{r}_i\times (\vec{\omega}\times\vec{r}_i)$

Si, por simplicidad, consideramos la velocidad angular en la dirección del eje OZ

$\vec{\omega}=\omega_z\vec{k}\qquad \vec{\omega}\times\vec{r}_i=\omega_z(-y_i\vec{\imath}+x_i\vec{\jmath})$

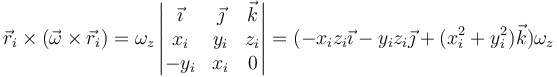
$\vec{r}_i\times (\vec{\omega}\times\vec{r}_i)=\omega_z\left|\begin{matrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ x_i & y_i & z_i \\ -y_i & x_i & 0\end{matrix}\right|=(-x_iz_i\vec{\imath}-y_iz_i\vec{\jmath}+(x_i^2+y_i^2)\vec{k})\omega_z$

Llevando esto al sumatorio nos queda, en función de los momentos y productos de inercia

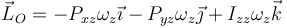
$\vec{L}_O=-P_{xz}\omega_z\vec{\imath}-P_{yz}\omega_z\vec{\jmath}+I_{zz}\omega_z\vec{k}$

De manera análoga se obtiene el resultado suponiendo una velocidad angular según el eje OX y según el eje OY. La solución general será una superposición de los tres casos.

$\vec{L}_O=(I_{xx}\omega_x-P_{xy}\omega_u-P_{xz}\omega_z)\vec{\imath}(-P_{xy}\omega_x+I_{yy}\omega_y-P_{yz}\omega_z)\vec{\jmath}+(-P_{xz}\omega_x-P_{yz}\omega_y+I_{zz}\omega_z)\vec{k}$

que podemos escribir en la forma matricial

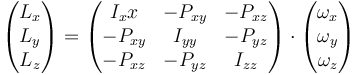
$\begin{pmatrix}L_x \\ L_y \\ L_z \end{pmatrix} = \begin{pmatrix} I_xx & -P_{xy} & -P_{xz} \\ -P_{xy} & I_{yy} & -P_{yz} \\ -P_{xz} & -P_{yz} & I_{zz}\end{pmatrix}\cdot\begin{pmatrix}\omega_x \\ \omega_y \\ \omega_z \end{pmatrix}$

la matriz que relaciona el momento cinético con la velocidad angular es una representación del tensor de inercia

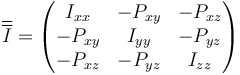
$\overline{\overline{I}} = \begin{pmatrix} I_{xx} & -P_{xy} & -P_{xz} \\ -P_{xy} & I_{yy} & -P_{yz} \\ -P_{xz} & -P_{yz} & I_{zz}\end{pmatrix}$

Este tensor nos permite calcular igualmente la energía cinética de rotación

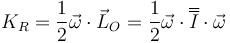
$K_R=\frac{1}{2}\vec{\omega}\cdot\vec{L}_O=\frac{1}{2}\vec{\omega}\cdot\overline{\overline{I}}\cdot\vec{\omega}$

Dado que la energía cinética es siempre positiva (o nula) se deduce que la matriz es simétrica y definida positiva.

7 Producto diádico y tensor de inercia

7.1 Definición de producto diádico

Adicionalmente al producto escalar y al producto vectorial entre dos vectores, se define un tercer tipo de producto, conocido como producto tensorial o producto diádico 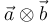$\vec{a}\otimes\vec{b}$ .

Este produycto diádico posee una representación sencilla en términos matriciales. Si un producto escalar puede representarse mediante el producto de un vector fila por un vector columna

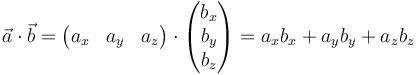
$\vec{a}\cdot\vec{b} = \begin{pmatrix}a_x & a_y & a_z\end{pmatrix}\cdot\begin{pmatrix}b_x \\ b_y \\ b_z\end{pmatrix}=a_xb_x+a_yb_y+a_zb_z$

el producto diádico puede representarse como el producto de un vector columna por un vector fila.

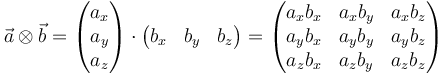
$\vec{a}\otimes\vec{b} = \begin{pmatrix}a_x \\ a_y \\ a_z\end{pmatrix}\cdot\begin{pmatrix}b_x & b_y & b_z\end{pmatrix}=\begin{pmatrix}a_x b_x & a_xb_y & a_x b_z \\ a_y b_x & a_y b_y & a_y b_z \\ a_z b_x & a_z b_y & a_z b_z\end{pmatrix}$

El producto diádico permite aislar elementos de una matriz, ya que al multiplicar dos vectores de la base resulta

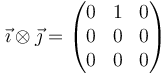
$\vec{\imath}\otimes\vec{\jmath}=\begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}$

Esto permite construir una base del espacio de las matrices 3×3 (equivalentes a tensores de segundo orden) y escribir cada tensor como una combinación lineal de ella

$\overline{\overline{A}}=\sum_{i,k}A_{ik} \vec{u}_i\otimes\vec{u}_k$

En particular el tensor unidad o identidad se expresará en forma diádica

$\overline{\overline{1}}=\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}=\vec{\imath}\otimes\vec{\imath}+\vec{\jmath}\otimes\vec{\jmath}+\vec{k}\otimes\vec{k}$

7.2 Propiedades del producto diádico

El producto diádico no es conmutativo, ya que al invertir el orden se obtiene la traspuesta de la matriz original.

Sí es distributivo,

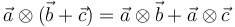
$\vec{a}\otimes(\vec{b}+\vec{c}) = \vec{a}\otimes\vec{b}+\vec{a}\otimes\vec{c}$

Puede multiplicarse escalarmente por un vector (lo que se denomina contraerse), resultando otro vector. El resultado depende de si se multiplica por la derecha o por la izquierda

$(\vec{a}\otimes\vec{b})\cdot\vec{c}=\vec{a}(\vec{b}\cdot\vec{c}) \qquad\qquad \vec{c}\cdot(\vec{a}\otimes\vec{b}))=(\vec{c}\cdot\vec{a})\vec{b}$

Esta relación permite escribir el producto de una matriz por un vector en forma de operaciones entre vectores.

7.3 Relación con el tensor de inercia

El cálculo del tensor de inercia se reduce a sumar, para todas las partículas

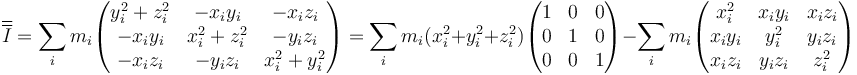
$\overline{\overline{I}}=\sum_i m_i\begin{pmatrix}y_i^2+z_i^2 & -x_iy_i & -x_iz_i\\ -x_iy_i & x_i^2+z_i^2 & -y_iz_i \\ -x_iz_i & -y_iz_i & x_i^2 + y_i^2\end{pmatrix}=\sum_i m_i(x_i^2+y_i^2+z_i^2)\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}-\sum_i m_i\begin{pmatrix}x_i^2 & x_iy_i & x_iz_i\\ x_iy_i & y_i^2 & y_iz_i \\ x_iz_i & y_iz_i & z_i^2\end{pmatrix}$

lo que se puede abreviar como

$\overline{\overline{I}}=\sum_i m_i|\vec{r}_i|^2\overline{\overline{1}}-\sum_i m_i(\vec{r}_i\otimes\vec{r}_i)$

Una vez calculado el sumatorio, el tensor de inercia se escribirá en la forma

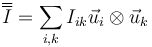
$\overline{\overline{I}}=\sum_{i,k}I_{ik}\vec{u}_i\otimes\vec{u}_k$

siendo las componentes diagonales los momentos de inercia y los no diagonales los productos de inercia cambiados de signo.

8 Ejes principales y momentos principales de inercia

Por las propiedades de las matrices simétricas definidas positivas, se tiene que el tensor de inercia tiene tres autovalores positivos (o nulos), denominados momentos principales de inercia, cuyos autovectores son ortogonales entre sí, apuntando en las ejes principales de inercia.

Es decir, existe una base ortonormal ligada al sólido 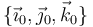$\{\vec{\imath}_0,\vec{\jmath}_0,\vec{k}_0\}$ tal que

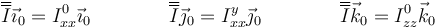
$\overline{\overline{I}}\vec{\imath}_0=I^0_{xx}\vec{\imath}_0\qquad\qquad \overline{\overline{I}}\vec{\jmath}_0=I^y_{xx}\vec{\jmath}_0 \qquad\qquad \overline{\overline{I}}\vec{k}_0=I^0_{zz}\vec{k}_0$

Esto quiere decir que en esta base, el tensor de inercia es diagonal, lo que se puede representar en la matriz

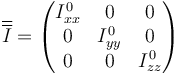
$\overline{\overline{I}}=\begin{pmatrix}I^0_{xx} & 0 & 0 \\ 0 & I^0_{yy} & 0 \\ 0 & 0 & I^0_{zz}\end{pmatrix}$

Usando la notación con productos diádicos

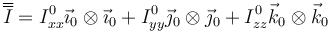
$\overline{\overline{I}}=I^0_{xx}\vec{\imath}_0\otimes\vec{\imath}_0+I^0_{yy}\vec{\jmath}_0\otimes\vec{\jmath}_0+I^0_{zz}\vec{k}_0\otimes\vec{k}_0$

En el sistema de ejes principales, el momento cinético posee una expresión más simple que en el caso general

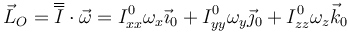
$\vec{L}_O =\overline{\overline{I}}\cdot\vec{\omega}= I_{xx}^0\omega_x\vec{\imath}_0 + I_{yy}^0\omega_y\vec{\jmath}_0 + I_{zz}^0\omega_z\vec{k}_0$

La determinación de los ejes principales puede hacerse por métodos algebraicos (resolviendo el problema de autovalores y autovectores), pero más a menudo se deducen por simple inspección, aprovechando las simetrías del sistema.

Ejes principales de un paralelepípedo

Siempre que tengamos un plano de simetría de un sólido, el eje perpndicular a él que pasa por el CM es un eje principal. Por ello, en un paralelepípedo de lados a, b y c, los ejes principales alrededor del CM son las rectas perpendiculares a las caras.

Ejes principales de una esfera

Por la simetría de la esfera, todos los ejes que pasan por su centro on principales, y alrededor de este punto el tensor de inercia no es solo diagonal, sino que es un múltiplo de la matriz unidad

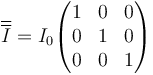
$\overline{\overline{I}}=I_0\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}$

Esto quiere decir que para la rotación de una esfera alrededor de su centro, el momento cinético es siempre proporcional a la velocidad angular.

$\vec{L}_O=I_0\vec{\omega}$

9 Rotación de ejes

@@ Línea 27: / Línea 27: @@
 Esta cantidad es proporcional a la velocidad angular en el sentido de que a doble velocidad angular le corresponde doble momento cinético. Sin embargo, en general ambos vectores no son paralelos, por lo que la relación no se reduce a multiplicar la velocidad angular por un número. En su lugar, la proporcionalidad se establece mediante un tensor, el cual se puede representar por una matriz, de manera que la relación entre las componentes del momento cinético y de la velocidad angular se puede escribir en la forma
-<center><math>\begin{pmatrix}L_{Ax}\\ L_{Ay}\\ L_{Az}\end{pmatrix}=\begin{pmatrix}I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix}\cdot\begin{pmatrix}\omega_{x}\\ \omega_{y}\\ \omega_{z}\end{pmatrix}</math></center>
+<center><math>\begin{pmatrix}L'_{Ax}\\ L'_{Ay}\\ L'_{Az}\end{pmatrix}=\begin{pmatrix}I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix}\cdot\begin{pmatrix}\omega_{x}\\ \omega_{y}\\ \omega_{z}\end{pmatrix}</math></center>
 o, en forma simbólica,
@@ Línea 46: / Línea 46: @@
 Esto nos da, para la componente x del momento cinético
-<center><math>L'_{Ax}=\sum_i m_i((x_i^2+y_i^2+z_i^2)\omega_x-(x_i\omega_x+y_i\omega_y+z_i\omega_z)x_i=
+<center><math>L'_{Ax}=\sum_i m_i((x_i^2+y_i^2+z_i^2)\omega_x-(x_i\omega_x+y_i\omega_y+z_i\omega_z)x_i)=
 \left(\sum_i m_i(y_i^2+z_i^2)\right)\omega_x +\left(-\sum_im_ix_iy_i\right)\omega_y+\left(-\sum_im_ix_iz_i\right)\omega_z</math></center>
-lo que nos permite identificar las componentes buscadas:
+Por otro lado, si desarrollamos la expresión matricial anterior queda, para la componente x
+<center><math>L'_{Ax}= I_{xx}\omega_x+I_{xy}\omega_y+I_{xz}\omega_z</math></center>
+lo que nos permite identificar las componentes buscadas, como los coeficientes de las componentes de la velocidad angular:
 <center><math>I_{xx}=\sum_i m_i(y_i^2+z_i^2)\qquad\qquad I_{xy}=-\sum_im_ix_iy_i\qquad\qquad I_{xz}= -\sum_im_ix_iz_i</math></center>