Resorte forzado
De Laplace
(→Frecuencia máxima) |
(→Frecuencia mínima) |
||
| Línea 96: | Línea 96: | ||
y obtenemos la frecuencia límite | y obtenemos la frecuencia límite | ||
<center> | <center> | ||
| - | <math>\omega_\mathrm{min}=\sqrt{\frac{k}{m}-\frac{kc}{m(y_0+c)}}=\omega_0\sqrt{\frac{y_0}{y_0+c}}=9. | + | <math>\omega_\mathrm{min}=\sqrt{\frac{k}{m}-\frac{kc}{m(y_0+c)}}=\omega_0\sqrt{\frac{y_0}{y_0+c}}=9.39\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
===Frecuencia máxima=== | ===Frecuencia máxima=== | ||
última version al 12:09 12 feb 2009
Contenido |
1 Enunciado
Un niño juega con un resorte de constante k = 20 N/m, longitud natural l0 = 5 cm y fricción despreciable del cual cuelga una masa m = 200 g, sujetando el otro extremo del resorte entre sus dedos, con la mano extendida horizontalmente. El niño agita la mano arriba y abajo, con una amplitud c = 2 cm y una frecuencia ω. Determine la posición de la pesa, si esta oscila con la misma frecuencia que la mano. ¿En qué condiciones la pesa llegará a golpearle la mano?
2 Solución
2.1 Movimiento de la pesa
El movimiento de la pesa es vertical, de forma que podemos usar una sola dimensión. Sea Y la dirección vertical y hacia abajo, medida desde la posición central de la mano, de forma que ésta ocupa la posición
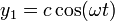
Obsérvese que ω es una frecuencia arbitraria (la que quiera darle el niño al mover su mano) y no tiene por qué coincidir con la que tendría el muelle si oscilara libremente (frecuencia propia)
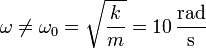
La pesa está sometida a la acción de dos fuerzas: su propio peso y la fuerza elástica ejercida por el muelle.
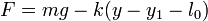
siendo l0 la longitud natural del muelle (que aquí debemos tener en cuenta porque queremos ver en qué caso el muelle se encoge del todo). La cantidad y1 aparece porque la ley de Hooke es dependiente del estiramiento total del muelle, y éste depende tanto de la posición inicial como de la final
La ecuación de movimiento para la pesa es entonces
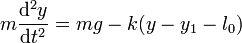
Sustituyendo y1 nos queda la ecuación de movimiento
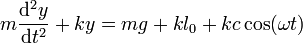
Sabemos que la pesa oscila con la misma frecuencia que la mano del niño. Estas oscilaciones las hará en torno a una cierta posición de equilibrio, así que la solución la podemos escribir en la forma
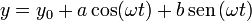
donde y0 (la posición central de las oscilaciones), a y b son constantes que hay que determinar. la razón de que haya que incluir un término en en el seno es que sabemos que oscila con frecuencia ω, pero no sabemos si existe un cierto desfase entre las oscilaciones de la mano y de la pesa. Una forma alternativa sería escribir
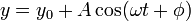
pero de esta forma el cálculo es un poco más complicado.
Sustituimos en la ecuación de movimiento y nos queda
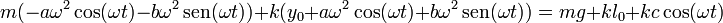
Si está ecuación debe cumplirse en todo instante, el coeficiente del coseno, el del seno, y el del término independiente deben ser iguales a un lado y a otro de la igualdad. Esto nos da tres ecuaciones:
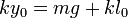
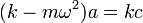
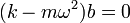
con lo que la solución para la posición de la pesa es
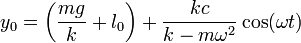
Resulta que
- La posición central es la misma que si no hubiera oscilaciones de la mano
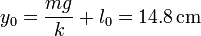
- El muelle se estira aproximadamente 10 cm sobre su longitud natural.
- La amplitud de las oscilaciones depende de la amplitud del movimiento de la mano, y de la frecuencia con que se hace
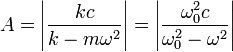
- Esta amplitud tiene un máximo (teóricamente infinito), justo a la frecuencia propia.
- A muy bajas frecuencias la amplitud coincide con al de oscialción de la mano (ya que ésta se mueve tan despacio que la pesa simplemente la sigue arriba y abajo)
- A altas frecuencias, la vibración de la mano es tan rápida que la pesa no es capaz de seguirla y su amplitud de oscilación tiende a 0.
- El desfase
 depende de si la frecuencia es menor o mayor que la frecuencia propia.
depende de si la frecuencia es menor o mayor que la frecuencia propia.
- Si ω < ω0 la constante a es positiva, lo que implica
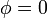 y la pesa oscila en fase con la mano, cuando la mano sube, la pesa sube, y si baja, la pesa baja.
y la pesa oscila en fase con la mano, cuando la mano sube, la pesa sube, y si baja, la pesa baja.
- Si ω > ω0 la constante a es negativa, lo que implica
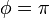 y la pesa oscila en contrafase con la mano: cuando la mano sube, la pesa baja, y viceversa.
y la pesa oscila en contrafase con la mano: cuando la mano sube, la pesa baja, y viceversa.
- Si ω < ω0 la constante a es positiva, lo que implica
La pesa chocará con la mano cuando la posición de la pesa y de la mano coincidan, esto es
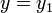

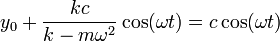
Para que este choque se produzca, la amplitud de oscilación debe ser lo suficientemente grande, lo cual solo ocurre cerca de la frecuencia propia (o frecuencia de resonancia). Habrá entonces una frecuencia mínima a la cual se producirá este choque, y también una frecuencia máxima.
Vamos a calcular estas dos frecuencias límite.
2.2 Frecuencia mínima
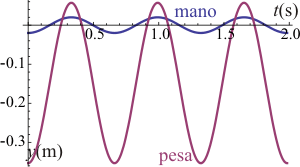
Si la frecuencia es menor que la frecuencia propia, la pesa oscila en fase con la mano, esto es, que si la mano sube la pesa también, y lo mismo si baja. Pero, dependiendo de la frecuencia, la amplitud de estas oscilaciones irá aumentando, y la frecuencia mínima se alcanzará cuando la pesa toque una sola vez a la mano.
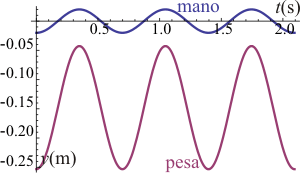
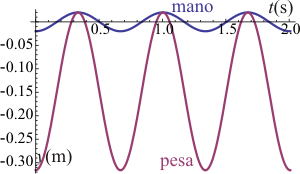
| 
| 
|
| ω < ωmin | ω = ωmin | ω > ωmin |
Esta colisión, de producirse, ocurrirá cuando la mano esté en su punto más alto, momento en que la pesa también estará en su punto superior. Esto ocurre para t = T / 2 (o t = nT + T / 2).
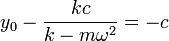
y obtenemos la frecuencia límite
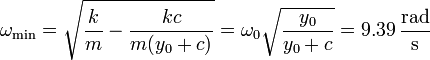
2.3 Frecuencia máxima
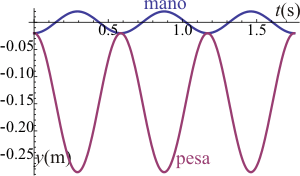
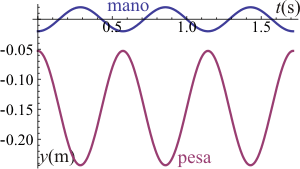
Según hemos dicho cuando la frecuencia es mayor que la frecuencia propia ω0, la pesa oscila al revés que la mano, si una sube, la otra baja. A frecuencias altas , la pesa nunca llega a la altura de la mano. A frecuencias menores que la de resonancia, la oscilación (teórica) de la pesa, corta dos veces por periodo a la de la mano. La posición extrema en que se produce la colisión es aquella en que la mano está en su punto más bajo, y la pesa en su punto más alto. Esto ocurre en t = 0 (o t = nT)
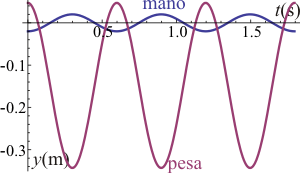
| 
| 
|
| ω < ωmax | ω = ωmax | ω > ωmax |
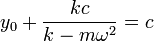
lo que nos da la frecuencia
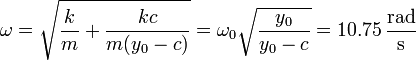
La banda de frecuencias es estrecha, la máxima corresponde a un periodo de 0.58 s, mientras que la mínima a uno de 0.67 s.






