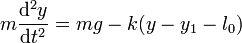Resorte forzado
De Laplace
(Nueva página: ==Enunciado== Un niño juega con un resorte de constante ''k'' = 20 N/m y fricción despreciable del cual cuelga una masa ''m'' = 200 g, sujetando el otro extremo del re...) |
|||
| Línea 4: | Línea 4: | ||
==Solución== | ==Solución== | ||
| + | El movimiento de la pesa es vertical, de forma que podemos usar una sola dimensión. Sea <math>Y</math> la dirección vertical y hacia abajo, medida desde la posición central de la mano, de forma que ésta ocupa la posición | ||
| + | |||
| + | <center><math>y_1 = b\cos(\omega t)\,</math></center> | ||
| + | |||
| + | La pesa está sometida a la acción de dos fuerzas: su propio peso y la fuerza elástica ejercida por el muelle. | ||
| + | |||
| + | <center><math>F = mg-k(y-y_1-l_0)</math></center> | ||
| + | |||
| + | siendo <math>l_0</math> la longitud natural del muelle (que aquí debemos tener en cuenta porque queremos ver en qué caso el muelle se encoge del todo). La cantidad y_1 aparece porque la ley de Hooke es dependiente del estiramiento total del muelle, y éste depende tanto de la posición inicial como de la final | ||
| + | |||
| + | La ecuación de movimiento para la pesa es entonces | ||
| + | |||
| + | <center><math>m\frac{\mathrm{d}^2y}{\mathrm{d}t^2}=mg-k(y-y_1-l_0)</math></center> | ||
| + | |||
| + | |||
| + | |||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 10:00 10 feb 2009
1 Enunciado
Un niño juega con un resorte de constante k = 20 N/m y fricción despreciable del cual cuelga una masa m = 200 g, sujetando el otro extremo del resorte entre sus dedos, con la mano extendida horizontalmente. El niño agita la mano arriba y abajo, con una amplitud b = 2 cm y una frecuencia ω. Determine la posición de la pesa, si esta oscila con la misma frecuencia que la mano. ¿En qué condiciones la pesa llegará a golpearle la mano?
2 Solución
El movimiento de la pesa es vertical, de forma que podemos usar una sola dimensión. Sea Y la dirección vertical y hacia abajo, medida desde la posición central de la mano, de forma que ésta ocupa la posición
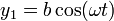
La pesa está sometida a la acción de dos fuerzas: su propio peso y la fuerza elástica ejercida por el muelle.
siendo l0 la longitud natural del muelle (que aquí debemos tener en cuenta porque queremos ver en qué caso el muelle se encoge del todo). La cantidad y_1 aparece porque la ley de Hooke es dependiente del estiramiento total del muelle, y éste depende tanto de la posición inicial como de la final
La ecuación de movimiento para la pesa es entonces