Campo de aceleraciones de un sólido
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con 'Derivando respecto al tiempo en la expresión del campo de velocidades obtenemos la aceleración de punto P <center><math>\vec{a}_{21}^P = \left.\frac{\mathrm{d}\vec{v}_{21}^P}…')
Edición más nueva →
(Página creada con 'Derivando respecto al tiempo en la expresión del campo de velocidades obtenemos la aceleración de punto P <center><math>\vec{a}_{21}^P = \left.\frac{\mathrm{d}\vec{v}_{21}^P}…')
Edición más nueva →
Revisión de 15:31 2 nov 2017
Derivando respecto al tiempo en la expresión del campo de velocidades obtenemos la aceleración de punto P
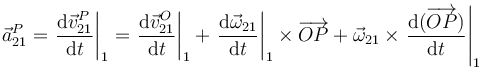
Siendo
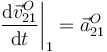
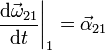
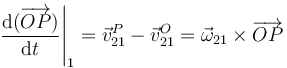
llegamos a la expresión del campo de aceleraciones
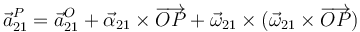
A diferencia del campo de velocidades, el campo de aceleraciones no es equiproyectivo:
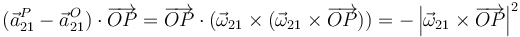
Solo en el caso de traslación o reposo instantáneos se cumplirá la equiproyectividad.
Dos consideraciones prácticas.
- El campo de aceleraciones requiere conocer tres vectores (esto es, 9 datos, frente a los 6 del campo de velocidades):
- La aceleración de un punto O,
.
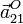- La velocidad angular instantánea,
.
- La aceleración angular,
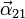, derivada temporal de la velocidad angular.
- La aceleración de un punto O,
- La aceleración de un punto P se puede calcular derivando la velocidad sólo si se conoce ésta como función del tiempo
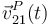. Conocerla en un instante no es suficiente.
El conocimiento del campo de aceleraciones es especialmente útil cuando tenemos un punto fijo O, para el cual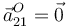 
y deseamos hallar la aceleración de otro punto en concreto, en particular, del centro de masas del sólido.
