Caso de movimiento circular
De Laplace
(→Aceleración tangencial) |
|||
| Línea 2: | Línea 2: | ||
Una partícula describe un movimiento circular de radio <math>R</math>, tal que su velocidad angular instantánea cumple | Una partícula describe un movimiento circular de radio <math>R</math>, tal que su velocidad angular instantánea cumple | ||
| - | <center><math>\omega = k\ | + | <center><math>\omega = k\theta\,</math></center> |
| - | con <math>k</math> una constante y <math>\ | + | con <math>k</math> una constante y <math>\theta</math> el ángulo que el vector de posición instantánea forma con el eje OX. |
| - | # Determine la aceleración angular de la partícula como función del ángulo <math>\ | + | # Determine la aceleración angular de la partícula como función del ángulo <math>\theta</math>. |
| - | # Halle las componentes intrínsecas de la aceleración lineal en <math>\ | + | # Halle las componentes intrínsecas de la aceleración lineal en <math>\theta = \pi/2</math> y <math>\theta = \pi</math>. |
| - | # Determine la ley horaria <math>\ | + | # Determine la ley horaria <math>\theta = \theta(t)</math>. |
<center>[[Archivo:particula-circunferencia-phi.png]]</center> | <center>[[Archivo:particula-circunferencia-phi.png]]</center> | ||
| Línea 15: | Línea 15: | ||
Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular | Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular | ||
| - | <center><math>\alpha = \dot{\omega} = k\dot{\ | + | <center><math>\alpha = \dot{\omega} = k\dot{\theta}</math></center> |
| - | debemos escribir <math>\dot{\ | + | debemos escribir <math>\dot{\theta}</math> como función del propio ángulo <math>\theta</math>, como nos pide el enunciado. Esto lo hacemos simplemente observando que la derivada temporal del ángulo girado no es otra que la velocidad angular |
| - | <center><math>\dot{\ | + | <center><math>\dot{\theta} = \frac{\mathrm{d}\theta}{\mathrm{d}t} = \omega = k\theta</math></center> |
así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida | así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida | ||
| - | <center><math>\alpha = k^2\ | + | <center><math>\alpha = k^2\theta\,</math></center> |
En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro | En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro | ||
| - | <center><math>\vec{\alpha} = \alpha\vec{k} = k^2\ | + | <center><math>\vec{\alpha} = \alpha\vec{k} = k^2\theta\vec{k}</math></center> |
==Componentes intrínsecas de la aceleración== | ==Componentes intrínsecas de la aceleración== | ||
| Línea 39: | Línea 39: | ||
siendo el módulo de la velocidad | siendo el módulo de la velocidad | ||
| - | <center><math>|\vec{v}| = \omega R = kR\ | + | <center><math>|\vec{v}| = \omega R = kR\theta</math></center> |
Derivando respecto al tiempo | Derivando respecto al tiempo | ||
| - | <center><math>a_t = kR \dot{\ | + | <center><math>a_t = kR \dot{\theta}= kR\omega = k^2R\theta</math></center> |
===Aceleración normal=== | ===Aceleración normal=== | ||
El valor de la aceleración normal es | El valor de la aceleración normal es | ||
| - | <center><math>a_n = \frac{|\vec{v}|^2}{R} = \frac{(kR\ | + | <center><math>a_n = \frac{|\vec{v}|^2}{R} = \frac{(kR\theta)^2}{R} = k^2R\theta^2</math></center> |
==Ley horaria== | ==Ley horaria== | ||
Podemos obtener la ley horaria aplicando de nuevo que, en un movimiento circular, la velocidad angular es igual a la derivada respecto al tiempo del ángulo que forma con el eje OX | Podemos obtener la ley horaria aplicando de nuevo que, en un movimiento circular, la velocidad angular es igual a la derivada respecto al tiempo del ángulo que forma con el eje OX | ||
| - | <center><math>\frac{\mathrm{d}\ | + | <center><math>\frac{\mathrm{d}\theta}{\mathrm{d}t}=k\theta</math></center> |
| - | Esta es una ecuación diferencial en cuanto a que para hallar <math>\ | + | Esta es una ecuación diferencial en cuanto a que para hallar <math>\theta(t)</math> por integración necesitamos conocer <math>\theta(t)</math>, que es justamente lo que deseamos calcular. |
En este caso, esta ecuación se resuelve de forma sencilla, observando que se trata de una ecuación ''separable''. Lo que nos dice esta ecuación es que el incremento diferencial en el ángulo, para un punto dado, es proporcional al valor del ángulo en dicho punto | En este caso, esta ecuación se resuelve de forma sencilla, observando que se trata de una ecuación ''separable''. Lo que nos dice esta ecuación es que el incremento diferencial en el ángulo, para un punto dado, es proporcional al valor del ángulo en dicho punto | ||
| - | <center><math>\mathrm{d}\ | + | <center><math>\mathrm{d}\theta = k\theta\,\mathrm{d}t</math></center> |
Ahora bien, esta ecuación la podemos leer también como que el tiempo necesario para incrementar el ángulo es inversamente proporcional al valor de éste | Ahora bien, esta ecuación la podemos leer también como que el tiempo necesario para incrementar el ángulo es inversamente proporcional al valor de éste | ||
| - | <center><math>\mathrm{d}t = \frac{\mathrm{d}\ | + | <center><math>\mathrm{d}t = \frac{\mathrm{d}\theta}{k\theta}</math></center> |
Para hallar el tiempo total en variar el ángulo una cantidad finita simplemente sumamos los diferenciales, esto es, integramos, | Para hallar el tiempo total en variar el ángulo una cantidad finita simplemente sumamos los diferenciales, esto es, integramos, | ||
| - | <center><math>\int_0^t \mathrm{d}t = \frac{1}{k}\int_{\ | + | <center><math>\int_0^t \mathrm{d}t = \frac{1}{k}\int_{\theta_0}^\theta \frac{\mathrm{d}\theta}{\theta}</math></center> |
lo que nos da la relación | lo que nos da la relación | ||
| - | <center><math>t = \frac{1}{k}\ln\left(\frac{\ | + | <center><math>t = \frac{1}{k}\ln\left(\frac{\theta}{\theta_0}\right)</math></center> |
| - | Nótese que no podemos hacer <math>\ | + | Nótese que no podemos hacer <math>\theta_0=0</math> porque ello haría infinito el logaritmo. |
Podemos invertir esta relación para escribir la ley horaria | Podemos invertir esta relación para escribir la ley horaria | ||
| - | <center><math>\ | + | <center><math>\theta(t) = \theta_0\mathrm{e}^{kt}</math></center> |
Vemos que el ángulo crece exponencialmente con el tiempo, por lo que la rapidez y la aceleración van incrementándose progresivamente, según hemos visto. | Vemos que el ángulo crece exponencialmente con el tiempo, por lo que la rapidez y la aceleración van incrementándose progresivamente, según hemos visto. | ||
última version al 15:44 10 oct 2017
Contenido |
1 Enunciado
Una partícula describe un movimiento circular de radio R, tal que su velocidad angular instantánea cumple
con k una constante y θ el ángulo que el vector de posición instantánea forma con el eje OX.
- Determine la aceleración angular de la partícula como función del ángulo θ.
- Halle las componentes intrínsecas de la aceleración lineal en θ = π / 2 y θ = π.
- Determine la ley horaria θ = θ(t).
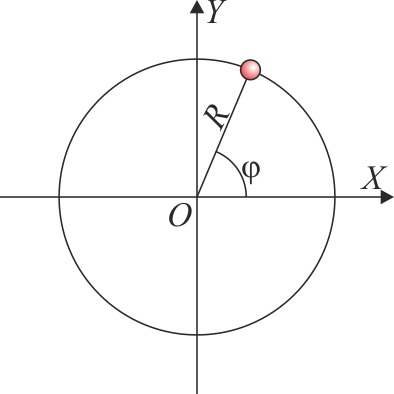
2 Aceleración angular
Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular
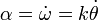
debemos escribir 
como función del propio ángulo θ, como nos pide el enunciado. Esto lo hacemos simplemente observando que la derivada temporal del ángulo girado no es otra que la velocidad angular
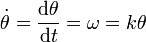
así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida
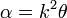
En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro
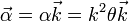
3 Componentes intrínsecas de la aceleración
Tenemos dos componentes intrínsecas de la aceleración:
3.1 Aceleración tangencial
Puesto que el movimiento no es uniforme, existe una aceleración tangencial igual a la derivada temporal de la rapidez
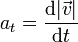
siendo el módulo de la velocidad
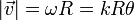
Derivando respecto al tiempo
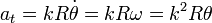
3.2 Aceleración normal
El valor de la aceleración normal es
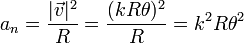
4 Ley horaria
Podemos obtener la ley horaria aplicando de nuevo que, en un movimiento circular, la velocidad angular es igual a la derivada respecto al tiempo del ángulo que forma con el eje OX
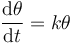
Esta es una ecuación diferencial en cuanto a que para hallar θ(t) por integración necesitamos conocer θ(t), que es justamente lo que deseamos calcular.
En este caso, esta ecuación se resuelve de forma sencilla, observando que se trata de una ecuación separable. Lo que nos dice esta ecuación es que el incremento diferencial en el ángulo, para un punto dado, es proporcional al valor del ángulo en dicho punto
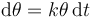
Ahora bien, esta ecuación la podemos leer también como que el tiempo necesario para incrementar el ángulo es inversamente proporcional al valor de éste
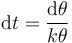
Para hallar el tiempo total en variar el ángulo una cantidad finita simplemente sumamos los diferenciales, esto es, integramos,
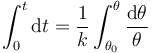
lo que nos da la relación
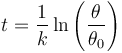
Nótese que no podemos hacer θ0 = 0 porque ello haría infinito el logaritmo.
Podemos invertir esta relación para escribir la ley horaria
Vemos que el ángulo crece exponencialmente con el tiempo, por lo que la rapidez y la aceleración van incrementándose progresivamente, según hemos visto.
Otra forma de hallar la solución de la ecuación diferencial consiste en buscar una función cuya derivada sea proporcional a ella misma. Esta función es naturalmente una exponencial.
Conocida la ley horaria, podríamos hallar la velocidad angular, la aceleración angular y la aceleración lineal como funciones del tiempo, simplemente derivando.
