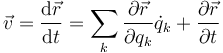Velocidad de una partícula (CMR)
De Laplace
(Página creada con '==Definición== Se define la velocidad media en un intervalo de tiempo como el cociente entre el desplazamiento realizado y el intervalo de tiempo empleado en realizarlo. <cent…') |
|||
| Línea 15: | Línea 15: | ||
<center><math>\vec{r}(t)=\vec{r}_0+\int_0^t \vec{v}\,\mathrm{d}t</math></center> | <center><math>\vec{r}(t)=\vec{r}_0+\int_0^t \vec{v}\,\mathrm{d}t</math></center> | ||
| - | + | ==Vector tangente== | |
El vector velocidad va en la dirección tangente a la trayectoria. Esto permite definir el unitario tangente | El vector velocidad va en la dirección tangente a la trayectoria. Esto permite definir el unitario tangente | ||
<center><math>\vec{T}=\frac{\vec{v}}{\left|\vec{v}\right|}\qquad\Rightarrow\qquad \vec{v}=\left|\vec{v}\right| \vec{T}</math></center> | <center><math>\vec{T}=\frac{\vec{v}}{\left|\vec{v}\right|}\qquad\Rightarrow\qquad \vec{v}=\left|\vec{v}\right| \vec{T}</math></center> | ||
| - | + | ==Rapidez y distancia recorrida== | |
Al módulo de la velocidad se lo denomina ''rapidez'' o ''celeridad'' de la partícula. Mide el ritmo con el que se recorre la trayectoria y como tal se relaciona directamente con el parámetro arco | Al módulo de la velocidad se lo denomina ''rapidez'' o ''celeridad'' de la partícula. Mide el ritmo con el que se recorre la trayectoria y como tal se relaciona directamente con el parámetro arco | ||
| Línea 30: | Línea 30: | ||
<center><math>s = s_0+\int_0^t \left|\vec{v}\right|\,\mathrm{d}t</math></center> | <center><math>s = s_0+\int_0^t \left|\vec{v}\right|\,\mathrm{d}t</math></center> | ||
| - | + | ==Componentes de la velocidad== | |
En un sistema de referencia fijo, los vectores de la base cartesiana son constantes, por lo que | En un sistema de referencia fijo, los vectores de la base cartesiana son constantes, por lo que | ||
| Línea 37: | Línea 37: | ||
es decir, las componentes de la velocidad son las derivadas de las componentes de la posición. | es decir, las componentes de la velocidad son las derivadas de las componentes de la posición. | ||
| - | + | ==Velocidad en función de parámetros== | |
Si la posición no está dada explícitamente en función del tiempo, sino que conocemos la trayectoria en función de un parámetro θ para hallar la velocidad es preciso aplicar la regla de la cadena | Si la posición no está dada explícitamente en función del tiempo, sino que conocemos la trayectoria en función de un parámetro θ para hallar la velocidad es preciso aplicar la regla de la cadena | ||
| Línea 59: | Línea 59: | ||
<center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\sum_k \frac{\partial\vec{r}}{\partial q_k}\dot{q}_k+\frac{\partial\vec{r}}{\partial t}</math></center> | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\sum_k \frac{\partial\vec{r}}{\partial q_k}\dot{q}_k+\frac{\partial\vec{r}}{\partial t}</math></center> | ||
| + | |||
| + | ==Velocidad en polares, cilíndricas y esféricas== | ||
| + | ===Coordenadas cilíndricas=== | ||
Revisión de 12:37 2 oct 2017
Contenido |
1 Definición
Se define la velocidad media en un intervalo de tiempo como el cociente entre el desplazamiento realizado y el intervalo de tiempo empleado en realizarlo.
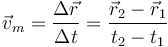
La velocidad instantánea de la partícula es el límite de la velocidad media cuando el intervalo de tiempo es muy pequeño
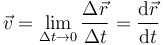
Es decir, la velocidad instantánea es la derivada de la posición respecto al tiempo. En Física, las derivadas respecto al tiempo suelen representarse con un punto sobre la magnitud
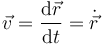
Si conocemos la velocidad instantánea a lo largo de un intervalo podemos calcular la posición como función del tiempo
2 Vector tangente
El vector velocidad va en la dirección tangente a la trayectoria. Esto permite definir el unitario tangente
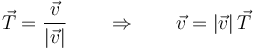
3 Rapidez y distancia recorrida
Al módulo de la velocidad se lo denomina rapidez o celeridad de la partícula. Mide el ritmo con el que se recorre la trayectoria y como tal se relaciona directamente con el parámetro arco
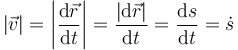
Esto permite determinar la distancia recorrida en un intervalo de tiempo dado
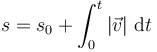
4 Componentes de la velocidad
En un sistema de referencia fijo, los vectores de la base cartesiana son constantes, por lo que
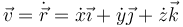
es decir, las componentes de la velocidad son las derivadas de las componentes de la posición.
5 Velocidad en función de parámetros
Si la posición no está dada explícitamente en función del tiempo, sino que conocemos la trayectoria en función de un parámetro θ para hallar la velocidad es preciso aplicar la regla de la cadena
A menudo, la posición no se indica en función de las coordenadas cartesianas, sino como función de 2 o más variables, θ, φ… (denominadas coordenadas generalizadas). En ese caso, se extiende la expresión anterior
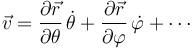
Si denominamos a las diferentes variables como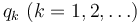 
la expresión anterior se escribe
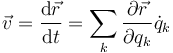
En ocasiones, la posición se expresa como función del tiempo y de una variable (dependiente implícitamente del tiempo). En ese caso, aplicamos que la derivada del tiempo respecto a sí mismo vale 1 (la velocidad del tiempo es un segundo por segundo) y queda
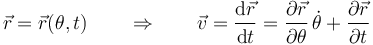
Nótese la diferencia entre la derivada total (d) y la parcial (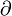
).
Si depende de varias variables y del tiempo queda la fórmula general
