Oscilador amortiguado

De Laplace

(Diferencias entre revisiones)

Antonio (Discusión | contribuciones)
(Nueva página: ==Enunciado== Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso <math>\mathbf{F}_r=-b \mathbf{v}</math>, de forma que su ecuación de movimiento, para un movimient...)
Edición más nueva →

Revisión de 20:24 8 feb 2009

1 Enunciado

Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso 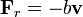$\mathbf{F}_r=-b \mathbf{v}$ , de forma que su ecuación de movimiento, para un movimiento unidimensional es

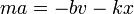
$ma =-b v-kx\,$

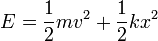
Demuestre que la energía mecánica $E=\frac{1}{2}mv^2+\frac{1}{2}kx^2$ es una función decreciente con el tiempo.
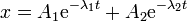
Si buscamos una solución particular de la forma $x = A e - λ t$ , calcule los dos valores que puede tener $λ$ . La solución general será una combinación de las dos posibilidades: $x = A_1 \mathrm{e}^{-\lambda_1 t}+A_2 \mathrm{e}^{-\lambda_2 t}\,$ con $A 1$ y $A 2$ dos constantes a determinar mediante las condiciones iniciales.
¿Cuál es el máximo valor de $b$ para que haya oscilaciones? ¿cómo es el movimiento si $b$ supera ese valor?
Considere el caso particular de una partícula de masa 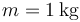$m=1\,\mathrm{kg}$ se encuentra sujeta a un muelle de constante 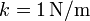$k=1\,\mathrm{N}/\mathrm{m}$ , existiendo un rozamiento $b$ . 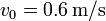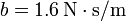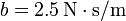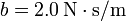Determine la posición en cualquier instante si se impulsa desde la posición de equilibrio con velocidad $v_0=0.6\,\mathrm{m}/\mathrm{s}$ si (a) $b = 1.6\,\mathrm{N}\cdot\mathrm{s}/\mathrm{m}$ $; (b) $b = 2.5\,\mathrm{N}\cdot\mathrm{s}/\mathrm{m}$ , (c) $b = 2.0\,\mathrm{N}\cdot\mathrm{s}/\mathrm{m}$ .