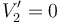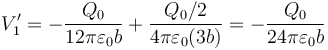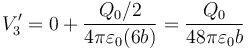Tres superficies conductoras concéntricas (GIE)
De Laplace
(Diferencias entre revisiones)
| Línea 19: | Línea 19: | ||
<center><math>V_1=\frac{-Q_0}{4\pi\varepsilon_0(2b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=-\frac{Q_0}{12\pi\varepsilon_0b}</math></center> | <center><math>V_1=\frac{-Q_0}{4\pi\varepsilon_0(2b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=-\frac{Q_0}{12\pi\varepsilon_0b}</math></center> | ||
| | ||
| - | <center><math>V_2=\frac{-Q_0}{4\pi\varepsilon_0(3b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=-\frac{Q_0}{ | + | <center><math>V_2=\frac{-Q_0}{4\pi\varepsilon_0(3b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=-\frac{Q_0}{24\pi\varepsilon_0b}</math></center> |
| | ||
<center><math>V_3=\frac{-Q_0}{4\pi\varepsilon_0(6b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=0</math></center> | <center><math>V_3=\frac{-Q_0}{4\pi\varepsilon_0(6b)}+\frac{Q_0}{4\pi\varepsilon_0(6b)}=0</math></center> | ||
===Campo=== | ===Campo=== | ||
| + | <center><math>\vec{E}(z=0)=\vec{0}</math></center> | ||
| + | | ||
| + | <center><math>\vec{E}\left(z=\frac{5b}{2}\right)=\frac{-Q_0}{4\pi\varepsilon_0(5b/2)^2}\vec{k}=-\frac{Q_0}{25\pi\varepsilon_0b^2}\vec{k}</math></center> | ||
| + | | ||
| + | <center><math>\vec{E}\left(z=4b\right)=\frac{-Q_0}{4\pi\varepsilon_0(4b)^2}\vec{k}=-\frac{Q_0}{64\pi\varepsilon_0b^2}\vec{k}</math></center> | ||
| + | | ||
| + | <center><math>\vec{E}\left(z=8b\right)=\vec{0}</math></center> | ||
| + | |||
===Energía=== | ===Energía=== | ||
| + | <center><math>U_e=\frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2+{1}{2}Q_3V_3=\frac{1}{2}Q_1V_1=\frac{Q_0^2}{24\pi\varepsilon_0b}</math></center> | ||
==Después de la conexión== | ==Después de la conexión== | ||
===Cargas y potenciales=== | ===Cargas y potenciales=== | ||
| + | ====Cargas==== | ||
| + | <center><math>Q_1=-Q_0\qquad\qquad Q_3=+Q_0</math></center> | ||
| + | | ||
| + | <center><math>0=V^\prime_2=-\frac{Q_0}{24\pi\varepsilon_0b}+\frac{Q_2}{4\pi\varepsilon_0(3b)}\qquad\Rightarrow\qquad Q_2=\frac{Q_0}{2}</math></center> | ||
| + | ====Potenciales==== | ||
| + | <center><math>V^\prime_2=0\,</math></center> | ||
| + | | ||
| + | <center><math>V^\prime_1=-\frac{Q_0}{12\pi\varepsilon_0b}+\frac{Q_0/2}{4\pi\varepsilon_0(3b)}=-\frac{Q_0}{24\pi\varepsilon_0b}</math></center> | ||
| + | | ||
| + | <center><math>V^\prime_3=0+\frac{Q_0/2}{4\pi\varepsilon_0(6b)}=\frac{Q_0}{48\pi\varepsilon_0b}</math></center> | ||
===Campo=== | ===Campo=== | ||
===Energía=== | ===Energía=== | ||
[[Categoría:Problemas de electrostática en presencia de materiales (GIE)]] | [[Categoría:Problemas de electrostática en presencia de materiales (GIE)]] | ||
Revisión de 20:09 8 may 2017
Contenido |
1 Enunciado
Se tiene un sistema formado por tres superficies conductoras esféricas concéntricas, de radios 2b, 3b y 6b. Inicialmente la esfera interior almacena una carga − Q0, la intermedia está aislada y descargada y la exterior almacena una carga + Q0.

- Calcule el potencial al que se encuentra cada esfera.
- Halle el campo eléctrico en los puntos del eje OZ siguientes: z = 0, z = 5b / 2, z = 4b y z = 8b, siendo el origen de coordenadas el centro de las esferas.
- Halle la energía almacenada en el sistema
En un momento dado se cierra el interruptor que conecta la esfera intermedia a tierra. Una vez que se alcanza de nuevo el equilibrio electrostático:
- ¿Cuáles son las nuevas cargas y potenciales de los tres conductores?
- ¿Cuánto vale ahora el campo eléctrico en los puntos del apartado 2?
- ¿Cuánto vale la energía almacenada en el sistema?
- ¿Cuánta energía se ha perdido en el proceso?
2 Antes de la conexión
2.1 Potenciales
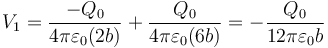
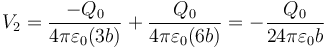
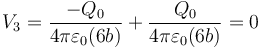
2.2 Campo

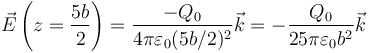

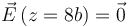
2.3 Energía
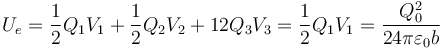
3 Después de la conexión
3.1 Cargas y potenciales
3.1.1 Cargas

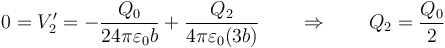
3.1.2 Potenciales