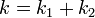Asociaciones de resortes
De Laplace
(Nueva página: ==Enunciado== Determine la frecuencia de oscilación de una masa <math>m</math> unida a dos muelles de constantes <math>k_1</math> y <math>k_2</math> cuando # los muelles están cone...) |
(→Muelles en paralelo) |
||
| Línea 19: | Línea 19: | ||
La fuerza total sobre la masa, resultante de las fuerzas aplicadas, vale | La fuerza total sobre la masa, resultante de las fuerzas aplicadas, vale | ||
| - | <center><math>F = F_1 + F_2 = -k_1x_1 - k_2x_2 = -k_1x-k_2x = -(k_1+k_2)x</math></center> | + | <center><math>F = F_1 + F_2 = -k_1x_1 - k_2x_2 = -k_1x-k_2x = -(k_1+k_2)x\,</math></center> |
Por tanto, la asociación se comporta como un solo muelle, cuya constante es la suma de las constantes | Por tanto, la asociación se comporta como un solo muelle, cuya constante es la suma de las constantes | ||
| - | <center><math>k = k_1 + k_2</math></center> | + | <center><math>k = k_1 + k_2\,</math></center> |
===Muelles en serie=== | ===Muelles en serie=== | ||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 16:40 8 feb 2009
Contenido |
1 Enunciado
Determine la frecuencia de oscilación de una masa m unida a dos muelles de constantes k1 y k2 cuando
- los muelles están conectados en paralelo.
- los muelles están conectados en serie.
2 Solución
Previamente al cálculo hay que definir qué entendemos por asociación en serie o en paralelo. El concepto es análogo al de las asociaciones de elelemntos en un circuito. Dos resortes estarán
- en paralelo, cuando están conectados por sus dos extremos,
- en serie, cuando lo están solo por uno dellos y en el punto de conexión no hay conectado ningún resorte adicional.
2.1 Muelles en paralelo
Por simplicidad supondremos el caso unidimensional, aunque resultados análogos se tienen en el caso general tridimensional.
Suponemos una masa unida a un punto fijo a través de dos resortes, de constantes k1 y k2. Cuando la masa se desplaza una cantidad x, los dos muelles se estirarán en la misma cantidad
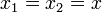
La fuerza total sobre la masa, resultante de las fuerzas aplicadas, vale
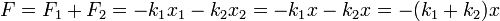
Por tanto, la asociación se comporta como un solo muelle, cuya constante es la suma de las constantes