Entrar Página Discusión Historial Go to the site toolbox

Error en el péndulo

De Laplace

(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Nueva página: ==Enunciado== Halle el error relativo cometido al calcular la velocidad para un péndulo en su punto más bajo empleando la aproximación de oscilador armónico, si se suelta en repos...)
Edición más nueva →

Revisión de 19:06 7 feb 2009

1 Enunciado

Halle el error relativo cometido al calcular la velocidad para un péndulo en su punto más bajo empleando la aproximación de oscilador armónico, si se suelta en reposo desde un ángulo respecto a la vertical de (a) 1° (b) 10° (c) 30° (d) 60° (e) 90°.

2 Solución

Un péndulo obedece la ecuación de movimiento

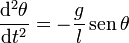
\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}=-\frac{g}{l}\,\mathrm{sen}\,\theta

siendo θ la inclinación respecto a la vertical (medida en radianes). Cuando esta separación es pequeña, se puede usar la aproximación

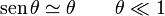
\mathrm{sen}\,\theta\simeq\theta \qquad\theta\ll 1

lo que reduce la ecuación del péndulo a la de un oscilador armónico

\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}\simeq-\frac{g}{l}\theta=-\omega^2\theta
Obtenido de "http://tesla.us.es/wiki/index.php/Error_en_el_p%C3%A9ndulo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace