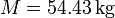Masa de un astronauta
De Laplace
(→Solución) |
|||
| Línea 12: | Línea 12: | ||
En el primer caso, la masa, que es la de la silla, es igual a | En el primer caso, la masa, que es la de la silla, es igual a | ||
| - | + | <center> | |
| - | <math>m = 605.6\left(\frac{0.90149}{2\pi}\right)^2\,\mathrm{kg} = 12.47\,\mathrm{kg}</math> | + | <math>m = 605.6\left(\frac{0.90149}{2\pi}\right)^2\,\mathrm{kg} = 12.47\,\mathrm{kg}</math></center> |
En el segundo caso, la masa total (silla más astronauta) es | En el segundo caso, la masa total (silla más astronauta) es | ||
| - | <math>m + M = 605.6\left(\frac{2.08832}{2\pi}\right)^2\,\mathrm{kg} = 66.90\,\mathrm{kg}</math> | + | <center><math>m + M = 605.6\left(\frac{2.08832}{2\pi}\right)^2\,\mathrm{kg} = 66.90\,\mathrm{kg}</math></center> |
de donde la masa del astronauta vale | de donde la masa del astronauta vale | ||
Revisión de 15:21 7 feb 2009
1 Enunciado
Para medir la masa de un astronauta en ausencia de gravedad se emplea un aparato medidor de masa corporal. Este aparato consiste, básicamente, en una silla que oscila en contacto con un resorte. El astronauta ha de medir su periodo de oscilación en la silla. En la segunda misión Skylab el resorte empleado tenía una constante k = 605.6 N/m y el periodo de oscilación de la silla vacía era de 0.90149 s. Calcule la masa de la silla. Con un astronauta en la silla el periodo medido fue 2.08832 s. Calcule la masa del astronauta.
2 Solución
El periodo de oscilación de un oscilador armónico es
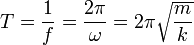
De aquí podemos despejar la masa
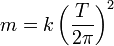
En el primer caso, la masa, que es la de la silla, es igual a
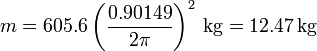
En el segundo caso, la masa total (silla más astronauta) es
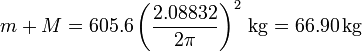
de donde la masa del astronauta vale