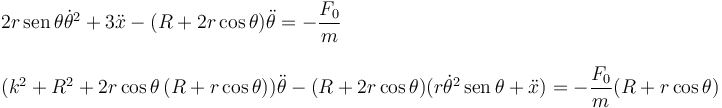Engranaje sobre cremallera (MR G.I.C.)
De Laplace
(Página creada con '= Enunciado = right La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un …') |
|||
| Línea 91: | Línea 91: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | == Ecuaciones de movimiento == | ||
| + | Escogemos el conjunto de coordenadas generalizadas <math>{x,\,\theta}</math>. El motivo la coordenada <math>x_r</math> no aparece en la energía potencial. | ||
| + | |||
| + | === Energía cinética === | ||
| + | |||
| + | ==== Cremallera ==== | ||
| + | Es una traslación pura. Tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | T_0 = \dfrac{1}{2}m\dot{x}_r^2 = | ||
| + | \dfrac{1}{2}m(\dot{x} -\dot{\theta}\,(R+r\cos\theta)). | ||
| + | </math> | ||
| + | </center> | ||
| + | ==== Deslizador ==== | ||
| + | También es una traslación pura. Entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | T_3 = \dfrac{1}{2}m\dot{x}^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | ==== Disco ==== | ||
| + | Pasamos por el centro de masas | ||
| + | <center> | ||
| + | <math> | ||
| + | T_2 = \dfrac{1}{2}m|\vec{v}^{\,A}_{21}|^2 + \dfrac{1}{2}I|\vec{\omega}_{21}|^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | La velocidad del centro es | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{ll} | ||
| + | \vec{v}^{\,A}_{21} & = \vec{v}^{\,A}_{20} + \vec{v}^{\,A}_{01},\\ | ||
| + | & \vec{v}^{\,A}_{20} = \vec{v}^{\,C}_{20} + \vec{\omega}_{20}\times\overrightarrow{CA} = R\dot{\theta}\,\vec{\imath}_1,\\ | ||
| + | & \vec{v}^{\,A}_{01} = \vec{v}_{01} = \dot{x}_r\,\vec{\imath}_1. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | \vec{v}^{\,A}_{21} = (\dot{x} -r\dot{\theta}\cos\theta)\,\vec{\imath}_1 | ||
| + | </math> | ||
| + | </center> | ||
| + | El momento de inercia es | ||
| + | <center> | ||
| + | <math> | ||
| + | I = mk^2, | ||
| + | </math> | ||
| + | </center> | ||
| + | donde <math>k</math> es el radio de giro del engranaje. Entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | T_2 = \dfrac{1}{2}m\,\left(k^2\dot{\theta}^2 + (\dot{x}-r\dot{\theta}\cos\theta)^2\right) | ||
| + | </math> | ||
| + | </center> | ||
| + | ==== Energía cinética total ==== | ||
| + | Haciendo la suma | ||
| + | <center> | ||
| + | <math> | ||
| + | T = T_0 + T_2 + T_3 = | ||
| + | \dfrac{1}{2}m\,\left( | ||
| + | 3\dot{x}^2 - 2(R+2r\cos\theta)\dot{x}\dot{\theta} + (k^2+R^2+2r\cos\theta(R+r\cos\theta))\dot{\theta}^2. | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | === Energía potencial === | ||
| + | La energía potencial gravitatoria es constante, pues los centros de masas de los tres sólidos se mueven siempre en horizontal. Podemos entonces obviar la energía potencial gravitatoria, pues al ser constante no va a contribuir en la ecuaciones de Lagrange. La única energía potencial relevante es la del muelle | ||
| + | <center> | ||
| + | <math> | ||
| + | U = \dfrac{1}{2}k\,(x-2R)^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | === Lagrangiana === | ||
| + | La función de Lagrange es | ||
| + | <center> | ||
| + | <math> | ||
| + | L = T-U = | ||
| + | \dot{x}^2 - 2(R+2r\cos\theta)\dot{x}\dot{\theta} + (k^2+R^2+2r\cos\theta(R+r\cos\theta))\dot{\theta}^2 - \dfrac{1}{2}k\,(x-2R)^2. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | === Fuerza generalizda === | ||
| + | Hay una fuerza no conservativa, <math>\vec{F}=-F_0\,\vec{\imath}_1</math>, actuando sobre la cremallera que va a dar una contribución a la fuerza generalizada. Tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | Q^{NC}_x = \vec{F}\cdot\dfrac{\partial\vec{v}_{01}}{\partial\dot{x}} | ||
| + | = | ||
| + | (-F_0\,\vec{\imath}_1)\cdot(\vec{\imath}_1) =-F_0\\ | ||
| + | \\ | ||
| + | Q^{NC}_{\theta} = \vec{F}\cdot\dfrac{\partial\vec{v}_{01}}{\partial\dot{\theta}} | ||
| + | = | ||
| + | (-F_0\,\vec{\imath}_1)\cdot(-(R+r\cos\theta)\,\vec{\imath}_1) = F_0(R+r\cos\theta). | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | === Ecuaciones de movimiento === | ||
| + | Escribimos ahora las ecuaciones de Lagrange | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{x}}\right) - \dfrac{\partial L}{\partial x} = Q^{NC}_x, | ||
| + | \\ | ||
| + | \\ | ||
| + | \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right) - \dfrac{\partial L}{\partial \theta} = Q^{NC}_{\theta}. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Haciendo las derivadas obtenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | 2r\,\mathrm{sen}\,\theta\dot{\theta}^2 + 3\ddot{x} - (R+2r\cos\theta)\ddot{\theta} = -\dfrac{F_0}{m} | ||
| + | \\ | ||
| + | \\ | ||
| + | (k^2+R^2+2r\cos\theta\,(R+r\cos\theta))\ddot{\theta} - (R+2r\cos\theta)(r\dot{\theta}^2\,\mathrm{sen}\,\theta + \ddot{x}) = -\dfrac{F_0}{m}(R+r\cos\theta) | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | [[Categoría:Problemas de mecánica analítica]] | ||
| + | [[Categoría:Problemas de Dinámica Analítica]] | ||
Revisión de 18:57 15 dic 2016
Contenido |
1 Enunciado
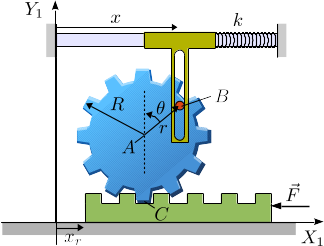
La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un deslizador con una ranura que desliza respecto al pasador en B. El deslizador está acoplado a un muelle, de constante elástica k, que se encuentra relajado cuando x = 2R. En ese instante se tiene θ = 0. Las masas del engranaje, el deslizador y la cremallera son mA, mS y mr, respectivamente. El contacto entre el pasador y la ranura es liso. El mecanismo es accionado por una fuerza aplicada sobe la cremallera como se indica en la figura.
- Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento.
- Encuentra las ecuaciones diferenciales del movimiento.
2 Solución
2.1 Grados de libertad
En el dibujo se identifican tres coordenadas: xr, x y θ. Sin embargo el problema tiene sólo dos grados de libertad. Podemos verlo a partir del número de ligaduras que se imponen entre los sólidos. Tenemos tres sólidos haciendo un movimiento plano, luego a priori hay 9 grados de libertad, 3 por cada sólido. Las ligaduras son
- {01}: traslación: 2 ligaduras.
- {31}: traslación: 2 ligaduras.
- {20}: rodadura sin deslizamiento en C: 2 ligaduras.
- {32}:
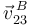 debe ser paralela a Y1: 1 ligadura.
debe ser paralela a Y1: 1 ligadura.
Esto hace en total 7 ligaduras. Por tanto el número de grados de libertad es
r = 9 − 7 = 2.
2.2 Relación entre las coordenadas
Vamos a obtener las reducciones cinemáticas de los movimientos relativos para encontrar la relación entre las ligaduras.
2.2.1 Movimiento {01}
Es la traslación de la cremallera respecto al suelo

Al ser una traslación no hay que especificar el punto en la velocidad.
2.2.2 Movimiento {31}
También es una traslación respecto al suelo

2.2.3 Movimiento {20}
Es una rodadura sin deslizamiento en C

2.2.4 Movimiento {23}
Este es el movimiento que nos va a dar la relación que buscamos. La ligadura es
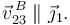
Usando composición de movimientos tenemos

Para cada movimiento tenemos
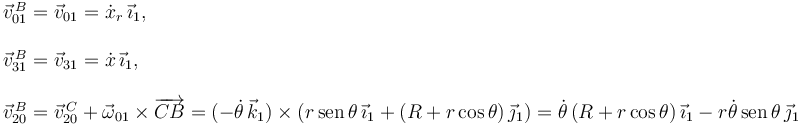
Entonces
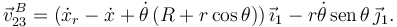
La componente en 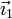 tiene que ser cero. Por tanto
tiene que ser cero. Por tanto
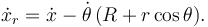
2.3 Ecuaciones de movimiento
Escogemos el conjunto de coordenadas generalizadas 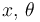 . El motivo la coordenada xr no aparece en la energía potencial.
. El motivo la coordenada xr no aparece en la energía potencial.
2.3.1 Energía cinética
2.3.1.1 Cremallera
Es una traslación pura. Tenemos
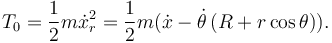
2.3.1.2 Deslizador
También es una traslación pura. Entonces
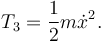
2.3.1.3 Disco
Pasamos por el centro de masas
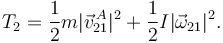
La velocidad del centro es

Entonces
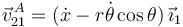
El momento de inercia es
I = mk2,
donde k es el radio de giro del engranaje. Entonces

2.3.1.4 Energía cinética total
Haciendo la suma
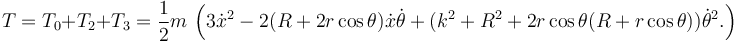
2.3.2 Energía potencial
La energía potencial gravitatoria es constante, pues los centros de masas de los tres sólidos se mueven siempre en horizontal. Podemos entonces obviar la energía potencial gravitatoria, pues al ser constante no va a contribuir en la ecuaciones de Lagrange. La única energía potencial relevante es la del muelle

2.3.3 Lagrangiana
La función de Lagrange es

2.3.4 Fuerza generalizda
Hay una fuerza no conservativa,  , actuando sobre la cremallera que va a dar una contribución a la fuerza generalizada. Tenemos
, actuando sobre la cremallera que va a dar una contribución a la fuerza generalizada. Tenemos

2.3.5 Ecuaciones de movimiento
Escribimos ahora las ecuaciones de Lagrange
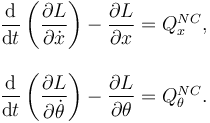
Haciendo las derivadas obtenemos