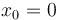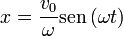Solución general del MAS
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Valor de ''a'' y ''b'') |
||
| Línea 20: | Línea 20: | ||
==Solución== | ==Solución== | ||
===Valor de ''a'' y ''b''=== | ===Valor de ''a'' y ''b''=== | ||
| + | Haciendo <math>t = 0</math> en la ley horaria, el resultado debe ser igual a la posición inicial | ||
| + | |||
| + | <center><math>x_0 = x(0) = a \cos(\omega\cdot 0) + b\,\mathrm{sen}\,(\omega\cdot 0) = a</math>{{tose}}<math>a = x_0\,</math></center> | ||
| + | |||
| + | Para hallar <math>b</math> necesitamos la velocidad. Derivando en la ley horaria | ||
| + | |||
| + | <center><math>v = \frac{\mathrm{d}x}{\mathrm{d}t}= -a\omega\,\mathrm{sen}\,(\omega t)+b\omega\cos(\omega t)</math></center> | ||
| + | |||
| + | y su valor en <math>t=0</math> nos da <math>b</math> | ||
| + | |||
| + | <center><math>v_0 = -a\omega\,\mathrm{sen}\,(\omega\cdot 0)+b\omega\cos(\omega\cdot 0) = b\omega</math> {{tose}} <math>b = \frac{v_0}{\omega}</math></center> | ||
| + | |||
| + | Por tanto, la posición en cualquier instante, en función de las condiciones iniciales, es | ||
| + | |||
| + | <center><math>x = x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}\,(\omega t)</math></center> | ||
| + | |||
| + | Como casos particulares tenemos | ||
| + | |||
| + | * el de una partícula que se libera desde una cierta posición en reposo | ||
| + | |||
| + | <center><math>v_0 = 0\,</math>{{qquad}}{{qquad}}<math>x= x_0\cos(\omega t)</math></center> | ||
| + | |||
| + | * el de una partícula a la que se comunica un impulso inicial en la posición de equilibrio | ||
| + | |||
| + | <center><math>x_0 = 0\,</math>{{qquad}}{{qquad}}<math>x= \frac{v_0}{\omega}\mathrm{sen}\,(\omega t)</math></center> | ||
| + | |||
===Amplitud y fase=== | ===Amplitud y fase=== | ||
===Velocidad=== | ===Velocidad=== | ||
Revisión de 22:52 6 feb 2009
Contenido |
1 Enunciado
La solución general de la ecuación de movimiento
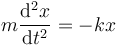
es de la forma
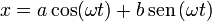
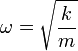
con a y b dos constantes dependientes de las condiciones iniciales.
- Halle el valor de las constantes a y b si la posición inicial de la partícula es x0 y su velocidad inicial es v0.
- Demuestre que la ecuación horaria
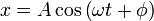es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes {A,φ} y las constantes {a,b}. Exprese A y φ en función de la posición y la velocidad iniciales, x0 y v0.
- Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales.
- Demuestre que la cantidad E = mv2 / 2 + kx2 / 2 no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales?
- Demuestre que x = ejωt, con
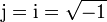, la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación
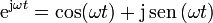
2 Solución
2.1 Valor de a y b
Haciendo t = 0 en la ley horaria, el resultado debe ser igual a la posición inicial
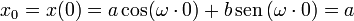
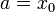
Para hallar b necesitamos la velocidad. Derivando en la ley horaria
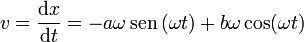
y su valor en t = 0 nos da b
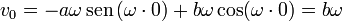
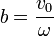
Por tanto, la posición en cualquier instante, en función de las condiciones iniciales, es
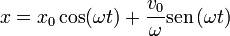
Como casos particulares tenemos
- el de una partícula que se libera desde una cierta posición en reposo
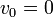x = x0cos(ωt)- el de una partícula a la que se comunica un impulso inicial en la posición de equilibrio
