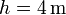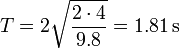Pelota que bota y bota
De Laplace
(Nueva página: ==Enunciado== Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde energía debido a la re...) |
|||
| Línea 4: | Línea 4: | ||
==Solución== | ==Solución== | ||
| + | Consideremos el momento inmediatamente posterior a un rebote en el suelo. En ese momento la pelota se encuentra en <math>y=0</math> y posee una velocidad hacia arriba <math>v_0</math>. La pelota sube y baja por acción de la gravedad y, si no hay rozamiento con el aire, cuando vuelve a tocar el suelo, su velocidad es <math>-v_0</math>. Si el rebote es elástico, la velocidad tras el rebote es la misma pero cambiada de signo, esto es, de nuevo <math>+v_0</math>. Por tanto, justo después del rebote vuelve a estar en <math>y=0</math> con velocidad <math>+v_0</math>, con lo que el proceso se vuelve a repetir y el movimiento resultante es periódico. | ||
| + | |||
| + | El periodo de este movimiento lo da el intervalo entre dos choques sucesivos 8despreciando el tiempo de la colisión). El movimiento que sigue la partícula es uniformemente acelerado | ||
| + | |||
| + | <center><math>y = v_0 t -\frac{1}{2}gt^2</math></center> | ||
| + | |||
| + | La pelota vuelve a tocar el suelo cuando <math>y=0</math> de nuevo | ||
| + | |||
| + | <center><math>0 = \left(v_0-\frac{1}{2}gt\right)t</math>{{tose}}<math>T = t = \frac{2v_0}{g}</math></center> | ||
| + | |||
| + | Queda relacionar este periodo con el dato del problema que, es la altura inicial. Esto lo podemos hacer a partir de la conservación de la energía mecánica. La energía mecánica inicial es toda mecánica. Justo antes del choque, toda la energía se ha convertido en cinética | ||
| + | |||
| + | <center><math>m g h = \frac{1}{2}mv_0^2</math>{{tose}} <math>v_0 = \sqrt{2gh}</math></center> | ||
| + | |||
| + | y el periodo del movimiento | ||
| + | |||
| + | <center><math>T = \frac{2v_0}{g}= 2\sqrt{\frac{2h}{g}}</math></center> | ||
| + | |||
| + | Para el caso particular <math>h = 4\,\mathrm{m}</math> | ||
| + | |||
| + | <center><math>T = 2\sqrt{\frac{2\cdot 4}{9.8}} = 1.81\,\mathrm{s}</math></center> | ||
| + | |||
| + | |||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 19:55 6 feb 2009
1 Enunciado
Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple?
2 Solución
Consideremos el momento inmediatamente posterior a un rebote en el suelo. En ese momento la pelota se encuentra en y = 0 y posee una velocidad hacia arriba v0. La pelota sube y baja por acción de la gravedad y, si no hay rozamiento con el aire, cuando vuelve a tocar el suelo, su velocidad es − v0. Si el rebote es elástico, la velocidad tras el rebote es la misma pero cambiada de signo, esto es, de nuevo + v0. Por tanto, justo después del rebote vuelve a estar en y = 0 con velocidad + v0, con lo que el proceso se vuelve a repetir y el movimiento resultante es periódico.
El periodo de este movimiento lo da el intervalo entre dos choques sucesivos 8despreciando el tiempo de la colisión). El movimiento que sigue la partícula es uniformemente acelerado
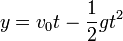
La pelota vuelve a tocar el suelo cuando y = 0 de nuevo
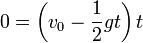


Queda relacionar este periodo con el dato del problema que, es la altura inicial. Esto lo podemos hacer a partir de la conservación de la energía mecánica. La energía mecánica inicial es toda mecánica. Justo antes del choque, toda la energía se ha convertido en cinética
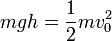

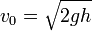
y el periodo del movimiento
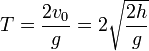
Para el caso particular