Péndulo que se tensa (CMR)
De Laplace
(Página creada con '==Enunciado== Una masa m está atada a un hilo flexible ideal de longitud l cuyo otro extremo se encuentra amarrado a un punto fijo O. Inicialmente la masa se encuentra sobre la…') |
|||
| Línea 8: | Línea 8: | ||
==Velocidad previa a la percusión== | ==Velocidad previa a la percusión== | ||
| + | Durante su descenso, la masa cae como una partícula no vinculada, sometida exclusivamente a la acción del peso. Puede aplicarse la ley de conservación de la energía mecánica, de manera que | ||
| + | <center><math>\frac{1}{2}m\left|\vec{v}^{\,-}\right|^2 = mgh \qquad\Rightarrow\qquad \left|\vec{v}^{\,-}\right|=\sqrt{2gh}</math></center> | ||
| + | siendo | ||
| + | |||
| + | <center><math>h=\sqrt{l^2-b^2}</math></center> | ||
| + | |||
| + | la altura que cae hasta que se tensa el hilo. | ||
| + | |||
| + | Si tomamos como eje OX el vertical hacia abajo y como eje OY el horizontal, el vector velocidad previa es | ||
| + | |||
| + | <center><math>\vec{v}^{\,-}=\sqrt{2gh}\vec{\imath}</math></center> | ||
==Velocidad posterior a la percusión== | ==Velocidad posterior a la percusión== | ||
| + | Cuando se tensa el hilo ya el movimiento pasa a ser circular. En el momento de la imposición de la ligadura aparece una tensión impulsiva, a lo largo del hilo. También puede aparecer una reacción vincular en el punto O donde está atado el péndulo. | ||
| + | |||
| + | Si tomamos el momento cinético en O la reacción en este punto no produce momento por estar aplicada en el propio punto y la tensión tampoco por ser radial. Por tanto | ||
| + | |||
| + | <center><math>\Delta \vec{L}_O=\vec{0}</math></center> | ||
| + | |||
| + | El valor previo es | ||
| + | |||
| + | <center><math>\vec{L}^{\,-}_O=m(h\vec{\imath}+b\vec{\jmath})\times(v^-\vec{\imath})=-mbv^{-}\vec{k}=-mb\sqrt{2gh}\vec{k}</math></center> | ||
| + | |||
| + | y el valor final, empleando coordenadas cilíndricas | ||
| + | |||
| + | <center><math>\vec{L}^{\,+}_O=m(l\vec{u}_\rho)\times(v^-\vec{u}_\varphi)=mlv^{+}\vec{k}</math></center> | ||
| + | |||
| + | Igualamos ambas cantidades y queda | ||
| + | |||
| + | <center><math>v^{+}=\frac{b}{l}v^{-}=-\frac{b}{l}\sqrt{2gh}</math></center> | ||
| + | |||
| + | Geométricamente, esto quiere decir que se pierde por completo la velocidad radial y queda solo la acimutal. | ||
| + | |||
==Percusión del hilo== | ==Percusión del hilo== | ||
==Altura máxima== | ==Altura máxima== | ||
[[Categoría:Problemas de mecánica de la partícula y de los sistemas (CMR)]] | [[Categoría:Problemas de mecánica de la partícula y de los sistemas (CMR)]] | ||
Revisión de 10:30 6 oct 2016
Contenido |
1 Enunciado
Una masa m está atada a un hilo flexible ideal de longitud l cuyo otro extremo se encuentra amarrado a un punto fijo O. Inicialmente la masa se encuentra sobre la horizontal del punto de anclaje y a una distancia b de éste (b < l). Se suelta la masa de forma que inicialmente cae verticalmente hasta que el hilo se tensa. A partir de ahí describe un movimiento pendular.
- ¿Cuál es la velocidad justo antes de que el hilo se tense?
- ¿Cuál es la velocidad justo después de la tensión del hilo?
- ¿Cuánto vale la percusión que ejerce el hilo en el momento de tensarse?
- ¿Hasta que altura vuelve a subir la masa?
2 Velocidad previa a la percusión
Durante su descenso, la masa cae como una partícula no vinculada, sometida exclusivamente a la acción del peso. Puede aplicarse la ley de conservación de la energía mecánica, de manera que

siendo
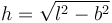
la altura que cae hasta que se tensa el hilo.
Si tomamos como eje OX el vertical hacia abajo y como eje OY el horizontal, el vector velocidad previa es
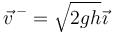
3 Velocidad posterior a la percusión
Cuando se tensa el hilo ya el movimiento pasa a ser circular. En el momento de la imposición de la ligadura aparece una tensión impulsiva, a lo largo del hilo. También puede aparecer una reacción vincular en el punto O donde está atado el péndulo.
Si tomamos el momento cinético en O la reacción en este punto no produce momento por estar aplicada en el propio punto y la tensión tampoco por ser radial. Por tanto

El valor previo es

y el valor final, empleando coordenadas cilíndricas
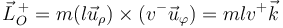
Igualamos ambas cantidades y queda
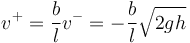
Geométricamente, esto quiere decir que se pierde por completo la velocidad radial y queda solo la acimutal.





