Energía de un sistema de partículas (CMR)
De Laplace
m |
|||
| Línea 44: | Línea 44: | ||
Un ejemplo sencillo lo tenemos en las fuerzas de rozamiento entre dos partes de un sistema mecánico. La fricción (debida a fuerzas puramente internas) produce calor, que se manifiesta en un aumento de la temperatura del sistema, esto es, en un incremento de la energía cinética total. | Un ejemplo sencillo lo tenemos en las fuerzas de rozamiento entre dos partes de un sistema mecánico. La fricción (debida a fuerzas puramente internas) produce calor, que se manifiesta en un aumento de la temperatura del sistema, esto es, en un incremento de la energía cinética total. | ||
| - | [[Categoría:Mecánica de los sistemas | + | [[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] |
Revisión de 08:53 1 oct 2016
1 Energía cinética
La energía cinética del sistema es la suma escalar de las energías cinéticas individuales
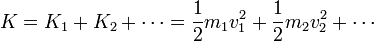
1.1 Descomposición de la energía cinética
Para la energía cinética podemos efectuar una descomposición análoga a la del momento cinético. Escribiendo cada velocidad como suma de la del CM más la relativa
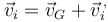
queda, para la energía cinética individual,
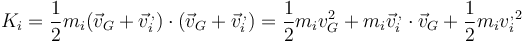
y para la energía cinética total
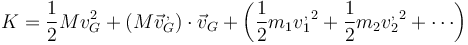
El segundo término se anula por aparecer en él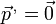 
, lo que reduce la energía cinética a
con
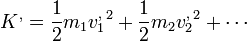
la energía cinética del sistema relativa al centro de masas.
Esta descomposición se interpreta como que el sistema posee una energía cinética por el movimiento de traslación colectivo, más un término debido al movimiento sobre sí mismo. Esta energía cinética intrínseca, K, es parte de la energía interna del sistema. Puede estar asociada a:
- un movimiento organizado. Por ejemplo, en la rotación de la Tierra alrededor de su eje.
- un movimiento desorganizado. Por ejemplo, en un gas que se encuentra a una cierta temperatura, el centro de masas puede estar estacionario y sin embargo el gas posee una energía cinética debido al movimiento de las moléculas que lo componen. Esta energía cinética es lo que llamamos agitación térmica.
- una combinación de ambos. Este es el caso general. La energía cinética del sistema parte se encuentra en movimientos macroscópicos (rotación o traslación de partes del sistema) y parte en movimientos microscópicos caóticos.
Por la presencia de estos términos microscópicos caóticos la energía cinética total del sistema es normalmente desconocida. En su lugar el estudio de los sistemas suele limitarse a la suma del término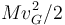 
con la suma de la energía cinética intrínseca debida a los movimientos macroscópicos (rotación, vibración, etc.).
2 Evolución de la energía cinética
Para la energía cinética no existe un teorema tan simple como para la cantidad de movimiento o el momento cinético. Operando del mismo modo que para estas dos cantidades, en sencillo probar que
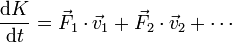
esto es, la derivada de la energía cinética es la potencia desarrollada por todas las fuerzas ejercidas en el sistema. Sin embargo, en este caso, no podemos eliminar las fuerzas internas de la ecuación. La razón es que las fuerzas internas sí pueden variar la energía cinética total.
Un ejemplo sencillo lo tenemos en las fuerzas de rozamiento entre dos partes de un sistema mecánico. La fricción (debida a fuerzas puramente internas) produce calor, que se manifiesta en un aumento de la temperatura del sistema, esto es, en un incremento de la energía cinética total.
