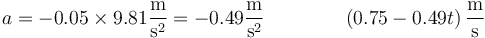Entrar Página Discusión Historial Go to the site toolbox

Moneda que va y vuelve

De Laplace

(Diferencias entre revisiones)
Línea 40: Línea 40:
<center><math>a = -\frac{F_r}{m}=-\mu g</math></center>
<center><math>a = -\frac{F_r}{m}=-\mu g</math></center>
-
===Velocidad del CM==
+
===Velocidad del CM===
Puesto que la aceleración es constante, la velocidad del CM es inmediata
Puesto que la aceleración es constante, la velocidad del CM es inmediata
Línea 66: Línea 66:
Sustituimos los datos del enunciado
Sustituimos los datos del enunciado
-
<center><math>a= -0.05\times 9.81\frac{\mathrm{m}}{\mathrm{s}^2}=-0.49\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>a= -0.05\times 9.81\frac{\mathrm{m}}{\mathrm{s}^2}=-0.49\frac{\mathrm{m}}{\mathrm{s}^2}\qquad\qquad \left(0.75-0.49t\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
-
 
+
&thinsp;
-
<center><math>v= \left(0.75-0.49t\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>\alpha= \frac{2a}{R}=-76.2\frac{1}{\mathrm{s}^2}\qquad\qquad\omega = \left(\omega_0-76.2 t\right)\frac{1}{\mathrm{s}}</math></center>
-
 
+
-
<center><math>\alpha= \frac{2a}{R}=-76.2\frac{1}{\mathrm{s}^2}</math></center>
+
-
 
+
-
<center><math>\omega = \left(\omega_0-76.2 t\right)\frac{1}{\mathrm{s}}</math></center>
+
==Velocidad del punto de contacto==
==Velocidad del punto de contacto==
-
==Condición de retroceso==g=9.81
+
==Condición de retroceso==

Revisión de 15:36 13 sep 2016

Contenido

1 Enunciado

Un conocido experimento casero es el de lanzar una moneda rodando y deslizando por un suelo horizontal y conseguir que retorne al lanzador. Supongamos que disponemos de una moneda de 2 euros (25.75 mm de diámetro, 8.50 g de masa) que podemos suponer un disco homogéneo. Se encuentra en posición vertical sobre una superficie horizontal en la que el coeficiente de rozamiento (estático y dinámico) vale μ = 0.05. 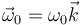Se lanza horizontalmente con una velocidad inicial de su centro G, \vec{v}_0=0.75\vec{\imath} m⁄s y una cierta velocidad angular inicial \vec{\omega}_0=\omega_0 \vec{k} que habrá que determinar, de forma que en el punto de contacto A la moneda rueda y desliza.

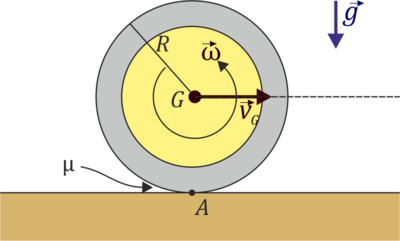
La moneda realiza un movimiento plano en todo momento.

  1. Determine la aceleración lineal del centro, 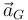\vec{a}_G y la aceleración angular de la moneda, 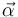\vec{\alpha}. A partir de ellas, calcule la velocidad lineal del centro y la velocidad angular del disco como funciones del tiempo.
  2. Calcule la velocidad de la moneda en el punto de contacto A como función del tiempo. Determine el instante en el que la moneda deja de deslizar y comienza a rodar sin deslizar. ¿Cuál es la velocidad del centro G del disco en ese instante?
  3. Determine el mínimo valor de ω0 por encima del cual la moneda retrocede y vuelve al lanzador. Para este valor de ω0, ¿Qué distancia recorre el centro de la moneda hasta que ésta deja de rodar?

Tómese g = 9.81ms2.

2 Aceleraciones y velocidades

Este problema es esencialmente el mismo que el de “Deslizamiento y rodadura de un disco”.

La moneda se mueve sometida a tres fuerzas:

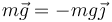  • Su peso, m\vec{g}=-mg\vec{\jmath}.
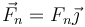  • La fuerza de reacción normal, \vec{F}_n=F_n\vec{\jmath}.
  • La fuerza de rozamiento por deslizamiento, \vec{F}_r=-F_r\vec{\imath}.

Estas fuerzas producen tanto aceleración del CM como aceleración angular del disco.

2.1 Aceleración lineal

Para el movimiento del CM tenemos

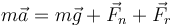
m\vec{a}=m\vec{g}+\vec{F}_n+\vec{F}_r

que separando por componentes nos da

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \left\{\begin{array}{rcl}ma & = & -F_r \\ 0 & = & -mg +F_n\end{\array}\right.

De aquí obtenemos la fuerza normal

F_n = mg\,

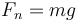
y dado que se trata de rozamiento por deslizamiento, también la fuerza de rozamiento

F_r=\mu F_n = \mu m g\,

lo que nos da la aceleración del CM

a = -\frac{F_r}{m}=-\mu g

2.2 Velocidad del CM

Puesto que la aceleración es constante, la velocidad del CM es inmediata

v(t) = v_0 + a t = v_0-\mu g t\,

2.3 Aceleración angular

Además de desplazarse, la moneda gira en torno a un eje perpendicular al plano de movimiento

\vec{\omega}=\omega\vec{k}\qquad\qquad \vec{\alpha}=\alpha\vec{k}

La única fuerza que produce un momento es la de rozamiento

I\vec{\alpha} = \overrightarrow{GG}\times(m\vec{g})+\overrightarrow{GA}\times\vec{F}_n+\overrightarrow{GA}\times\vec{F}_r=-F_rR\vec{k}

lo que nos da la aceleración angular

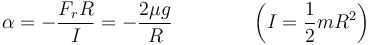
\alpha = -\frac{F_rR}{I}=-\frac{2\mu g}{R}\qquad\qquad \left(I=\frac{1}{2}m R^2\right)

2.4 Velocidad angular

Al ser también constante la aceleración angular, queda la velocidad angular

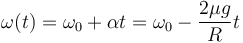
\omega(t)=\omega_0+\alpha t = \omega_0-\frac{2\mu g}{R}t

2.5 Valores numéricos

Sustituimos los datos del enunciado

a= -0.05\times 9.81\frac{\mathrm{m}}{\mathrm{s}^2}=-0.49\frac{\mathrm{m}}{\mathrm{s}^2}\qquad\qquad \left(0.75-0.49t\right)\frac{\mathrm{m}}{\mathrm{s}}

 

\alpha= \frac{2a}{R}=-76.2\frac{1}{\mathrm{s}^2}\qquad\qquad\omega = \left(\omega_0-76.2 t\right)\frac{1}{\mathrm{s}}


3 Velocidad del punto de contacto

4 Condición de retroceso

Obtenido de "http://tesla.us.es/wiki/index.php/Moneda_que_va_y_vuelve"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace