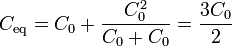Cuatro planos y fuente de tensión

De Laplace

Revisión de 13:30 15 ene 2009 (ver código fuente) Antonio (Discusión | contribuciones) ← Edición más antigua		Revisión de 14:07 15 ene 2009 (ver código fuente) Antonio (Discusión | contribuciones) (→Cargas, campos y potenciales) Edición más nueva →
Línea 10:		Línea 10:
	==Solución==		==Solución==
	===Cargas, campos y potenciales===		===Cargas, campos y potenciales===
-	El sistema de cuatro placas forma tres condensadores	+	Aunque el sistema está formado por cuatro placas, puede considerarse como formado por solo dos conductores, ya que las placas exteriores, que se encuentran permanentemente a tierra, funcionan simplemente como referencia, actuando como  6ldquo;el infinito” en un sistema arbitrario de conductores. Los únicos conductores “vivos”, en el sentido de que podemos variar sus potenciales o fijar sus cargas, son las dos placas centrales.
		+
		+	Considerado como un sistema de dos conductores, el circuito equivalente estará formado por tres condensadores. Puesto que la sección y la distancia entre placas son las mismas en todos los casos, las capacidades son todas iguales
		+
		+	<center><math>\overline{C}_{22}=\overline{C}_{23}=\overline{C}_{33}=C_0 = \frac{\varepsilon_0 L^2}{a}</math></center>
		+
		+	Aquí <math>\overline{C}_{22}</math> representa la capacidad que forma el conductor 2 con tierra, que en este caso es el conductor 1. Por ello, sería equivalente que pusiéramos <math>\overline{C}_{12}</math> o <math>\overline{C}_{22}</math> en este caso; lo mismo con <math>\overline{C}_{33}</math> y <math>\overline{C}_{34}</math>.
		+
		+	Esto nos da los coeficientes de capacidad
		+
		+	<center><math>C_{22} = \overline{C}_{22}+\overline{C}_{23} = 2C_0</math>{{qquad}}<math>C_{23}=C_{32}=-\overline{C}_{23} = -C_0</math>{{qquad}}<math>C_{33} = \overline{C}_{23}+\overline{C}_{33} = 2C_0</math></center>
		+
		+	o, en forma matricial
		+
		+
		+	Además de estos tres condensadores, lo único que hay que añadir es la fuente de tensión <math>V_0</math> y las conexiones a tierra de las placas exteriores. A la placa 3 no hace falta conectar nada, por estar aislada y descargada.
		+
		+	Para hallar la carga en la placa 2, simplemente observamos que se encuentra conectada a tierra por dos ramas, una con un solo condensador <math>C_0</math> y otra formada por dos condensadores <math>C_0</math> puestos en serie. La capacidad equivalente de la asociación será
		+
		+	<center><math>C_\mathrm{eq}=C_0+\frac{C_0^2}{C_0+C_0} = \frac{3C_0}{2}</math></center>
		+
	===Estado tras la conexión===		===Estado tras la conexión===
	===Carga transferida y trabajo===		===Carga transferida y trabajo===
	[[Categoría:Problemas de campo eléctrico en presencia de conductores]]		[[Categoría:Problemas de campo eléctrico en presencia de conductores]]

---

Revisión de 14:07 15 ene 2009

Contenido [ocultar] 1 Enunciado 2 Solución 2.1 Cargas, campos y potenciales 2.2 Estado tras la conexión 2.3 Carga transferida y trabajo

1 Enunciado

Se tiene un sistema formado por cuatro placas cuadradas de lado L, situadas paralelamente a una distancia $a$ cada una de la siguiente. Entre las placas hay vacío.

Las dos placas exteriores (“1” y “4”) se encuentran permanentemente a tierra.

1. Inicialmente, la placa 2 se encuentra conectada a un generador e tensión V₀ mientras que la 3 está aislada y descargada. Calcule el campo eléctrico en cada una de las tres regiones, la carga y el voltaje de las cuatro placas en este estado, así como la energía electrostática almacenada en el sistema.
2. De forma abrupta, sin dar tiempo a que las placas se descarguen, el interruptor se pasa de la posición A la B, pasando la fuente a estar conectada a la placa 3. Halle los nuevos valores de los campos, las cargas, las tensiones y la energía almacenada una vez que se ha alcanzado de nuevo el equilibrio electrostático.
3. Suponga que a la salida de la fuente de tensión se coloca un amperímetro y un integrador, de forma que se puede saber la carga que pasa por el cable durante el periodo transitorio. ¿Qué valor dará esta lectura? ¿Qué trabajo realiza la fuente durante este periodo transitorio?

2 Solución

2.1 Cargas, campos y potenciales

Aunque el sistema está formado por cuatro placas, puede considerarse como formado por solo dos conductores, ya que las placas exteriores, que se encuentran permanentemente a tierra, funcionan simplemente como referencia, actuando como 6ldquo;el infinito” en un sistema arbitrario de conductores. Los únicos conductores “vivos”, en el sentido de que podemos variar sus potenciales o fijar sus cargas, son las dos placas centrales.

Considerado como un sistema de dos conductores, el circuito equivalente estará formado por tres condensadores. Puesto que la sección y la distancia entre placas son las mismas en todos los casos, las capacidades son todas iguales

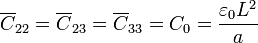
Aquí 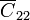representa la capacidad que forma el conductor 2 con tierra, que en este caso es el conductor 1. Por ello, sería equivalente que pusiéramos 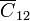o 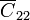en este caso; lo mismo con y .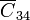

Esto nos da los coeficientes de capacidad

        

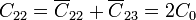
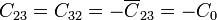
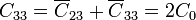
o, en forma matricial

Además de estos tres condensadores, lo único que hay que añadir es la fuente de tensión V₀ y las conexiones a tierra de las placas exteriores. A la placa 3 no hace falta conectar nada, por estar aislada y descargada.

Para hallar la carga en la placa 2, simplemente observamos que se encuentra conectada a tierra por dos ramas, una con un solo condensador C₀ y otra formada por dos condensadores C₀ puestos en serie. La capacidad equivalente de la asociación será

2.2 Estado tras la conexión

2.3 Carga transferida y trabajo