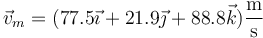Entrar Página Discusión Historial Go to the site toolbox

Movimiento con velocidades diferentes

De Laplace

(Diferencias entre revisiones)
Línea 29: Línea 29:
y
y
-
<center><math>\Delta \vec{r}_2=\vec{v}_2\,\Delta t_1=(60\vec{\imath}+80\vec{k})\frac{\mathrm{m}}{\mathrm{s}}\cdot 1500\,\mathrm{s}=(90\vec{\imath}+120\,\vec{\jmath})\mathrm{km}</math></center>
+
<center><math>\Delta \vec{r}_2=\vec{v}_2\,\Delta t_1=(60\vec{\imath}+80\vec{k})\frac{\mathrm{m}}{\mathrm{s}}\cdot 1500\,\mathrm{s}=(90\vec{\imath}+120\vec{k})\mathrm{km}</math></center>
siendo el desplazamiento total
siendo el desplazamiento total

Revisión de 16:58 26 ene 2016

Contenido

1 Enunciado

Una nave viaja por el espacio recorriendo 150 km con una velocidad 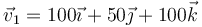\vec{v}_1=100\vec{\imath}+50\vec{\jmath}+100\vec{k} (m/s), da un quiebro instantáneo y recorre otros 150 km con velocidad 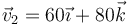\vec{v}_2=60\vec{\imath}+80\vec{k} (m/s). Calcule

  1. La distancia recorrida y la rapidez media.
  2. El desplazamiento y la velocidad media en el recorrido.
  3. Supongamos que el quiebro no es instantáneo, sino que lo hace con aceleración constante, empleando un tiempo de 25\,min en la maniobra. ¿Cuál es en ese caso el desplazamiento total y la velocidad media del trayecto?

2 Distancia y rapidez media

La distancia total recorrida es evidentemente 300 km. El tiempo empleado en recorrer cada tramo lo obtenemos a partir de la rapidez en cada uno.

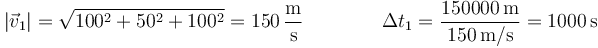
|\vec{v}_1| =\sqrt{100^2+50^2+100^2}=150\,\frac{\mathrm{m}}{\mathrm{s}}\qquad \qquad \Delta t_1 = \frac{150000\,\mathrm{m}}{150\,\mathrm{m}/\mathrm{s}}=1000\,\mathrm{s}

y

|\vec{v}_2| =\sqrt{60^2+80^2}=100\,\frac{\mathrm{m}}{\mathrm{s}}\qquad \qquad \Delta t_2 = \frac{150000\,\mathrm{m}}{100\,\mathrm{m}/\mathrm{s}}=1500\,\mathrm{s}

lo que da el intervalo total

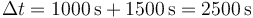
\Delta t = 1000\,\mathrm{s}+1500\,\mathrm{s}=2500\,\mathrm{s}

y la rapidez media

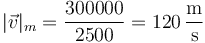
|\vec{v}|_m=\frac{300000}{2500}=120\,\frac{\mathrm{m}}{\mathrm{s}}

3 Desplazamiento y velocidad media

El desplazamiento en cada tramo lo hallamos a partir de la velocidad y el intervalo de tiempo de cada uno

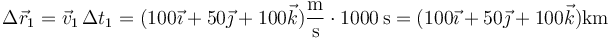
\Delta \vec{r}_1=\vec{v}_1\,\Delta t_1=(100\vec{\imath}+50\vec{\jmath}+100\vec{k})\frac{\mathrm{m}}{\mathrm{s}}\cdot 1000\,\mathrm{s}=(100\vec{\imath}+50\vec{\jmath}+100\vec{k})\mathrm{km}

y

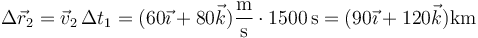
\Delta \vec{r}_2=\vec{v}_2\,\Delta t_1=(60\vec{\imath}+80\vec{k})\frac{\mathrm{m}}{\mathrm{s}}\cdot 1500\,\mathrm{s}=(90\vec{\imath}+120\vec{k})\mathrm{km}

siendo el desplazamiento total

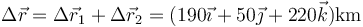
\Delta\vec{r}=\Delta\vec{r}_1+\Delta\vec{r}_2=(190\vec{\imath}+50\vec{\jmath}+220\vec{k})\mathrm{km}

y la velocidad media

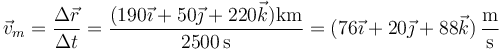
\vec{v}_m=\frac{\Delta \vec{r}}{\Delta t}=\frac{(190\vec{\imath}+50\vec{\jmath}+220\vec{k})\mathrm{km}}{2500\,\mathrm{s}}=(76\vec{\imath}+20\vec{\jmath}+88\vec{k})\,\frac{\mathrm{m}}{\mathrm{s}}

4 Movimiento acelerado

Si entre las dos velocidades hay un movimiento acelerado, con aceleración constante

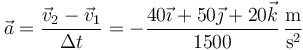
\vec{a}=\frac{\vec{v}_2-\vec{v}_1}{\Delta t}=-\frac{40\vec{\imath}+50\vec{\jmath}+20\vec{k}}{1500}\,\frac{\mathrm{m}}{\mathrm{s}^2}

En un movimiento de aceleración constante, la velocidad media en un intervalo es la media entre las velocidades en los extremos

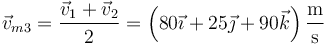
\vec{v}_{m3}=\frac{\vec{v}_1+\vec{v}_2}{2}=\left(80\vec{\imath}+25\vec{\jmath}+90\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}

por lo que el desplazamiento en este periodo intermedio es

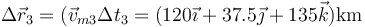
\Delta \vec{r}_3=(\vec{v}_{m3}\Delta t_3=(120\vec{\imath}+37.5\vec{\jmath}+135\vec{k})\mathrm{km}

Sumando esta cantidad al desplazamiento de los dos tramos rectos queda

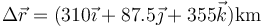
\Delta \vec{r}=(310\vec{\imath}+87.5\vec{\jmath}+355\vec{k})\mathrm{km}

siendo el intervalo de tiempo total

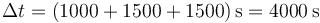
\Delta t = (1000+1500+1500)\,\mathrm{s}=4000\,\mathrm{s}

y la velocidad media

\vec{v}_m=(77.5\vec{\imath}+ 21.9\vec{\jmath}+88.8\vec{k})\frac{\mathrm{m}}{\mathrm{s}}
Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_con_velocidades_diferentes"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace