Entrar Página Discusión Historial Go to the site toolbox

Barra sujeta por un cable

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una mesa plegable está articulada a la pared por un extremo, y cuelga de la pared por un cable tirante. En dos dimensiones esto se puede modelar como una barra de…')
 
Línea 41: Línea 41:
Vemos que la suma de las tres fuerzas es nula
Vemos que la suma de las tres fuerzas es nula
-
<center>[[Archivo:barra-cable-tenso-02.png]]</center>
+
<center>[[Archivo:barra-cable-tenso-03.png]]{{qquad}}{{qquad}}[[Archivo:barra-cable-tenso-02.png]]</center>
y que también lo es la suma de sus momentos. Esto se puede comprobar observando que las tres rectas soporte son concurrentes en un punto O. Si tomamos el momento respecto a dicho punto el resultados es nulo.
y que también lo es la suma de sus momentos. Esto se puede comprobar observando que las tres rectas soporte son concurrentes en un punto O. Si tomamos el momento respecto a dicho punto el resultados es nulo.
-
 
-
<center>[[Archivo:barra-cable-tenso-03.png]]</center>
 
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]

última version al 16:04 26 ene 2016

1 Enunciado

Una mesa plegable está articulada a la pared por un extremo, y cuelga de la pared por un cable tirante. En dos dimensiones esto se puede modelar como una barra de longitud b y masa m distribuida uniformemente. La barra está articulada por su extremo A y atada por su extremo B a una pared vertical, de forma que el cable forma un ángulo de 45° con la vertical.

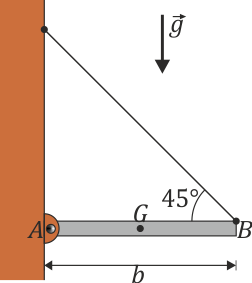
Archivo:barra-cable-tenso.png

Calcule la tensión del cable, así como la fuerza de reacción en el punto A.

2 Solución

Para que la barra esté en equilibrio deben cumplirse las ecuaciones de la estática del sólido rígido. Deben anularse la resultande de las fuerzas aplicadas y de los momentos de estas fuerzas.

\vec{F}=\vec{0}\qquad\qquad \vec{M}_O=\vec{0}

Las fuerzas aplicadas son:

  • El peso 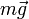m\vec{g} aplicado en el centro de la barra.
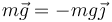
m\vec{g}=-mg\vec{\jmath}
  • La tensión del cable, 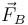\vec{F}_B aplicada en el extremo B y en la dirección del cable. Por formar éste un ángulo de 45° sus dos componentes son iguales
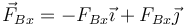
\vec{F}_{Bx}=-F_{Bx}\vec{\imath}+F_{Bx}\vec{\jmath}
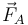
  • La reacción en el punto A, \vec{F}_A

Puesto que la barra está articulada en el punto A, en este punto no se ejerce ningún momento de reacción.

Como centro de reducción O tomamos el propio punto A. De esta forma, nos ahorramos de calcular el momento de esta fuerza de reacción.

La condición de que se anule el momento resultante en A nos da

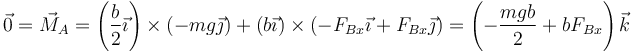
\vec{0}=\vec{M}_A=\left(\frac{b}{2}\vec{\imath}\right)\times(-mg\vec{\jmath})+\left(b\vec{\imath}\right)\times(-F_{Bx}\vec{\imath}+F_{Bx}\vec{\jmath})=\left(-\frac{mgb}{2}+bF_{Bx}\right)\vec{k}

Esto nos da la tensión

F_{Bx} = \frac{mg}{2} \qquad\qquad \vec{F}_B=\frac{mg}{2}\left(-\vec{\imath}+\vec{\jmath}\right)

Una vez que tenemos esta fuerza, la de reacción en A es inmediata

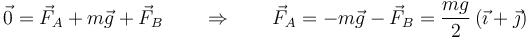
\vec{0}=\vec{F}_A+m\vec{g}+\vec{F}_B\qquad\Rightarrow\qquad \vec{F}_A=-m\vec{g}-\vec{F}_B=\frac{mg}{2}\left(\vec{\imath}+\vec{\jmath}\right)

Vemos que la suma de las tres fuerzas es nula

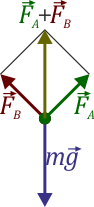
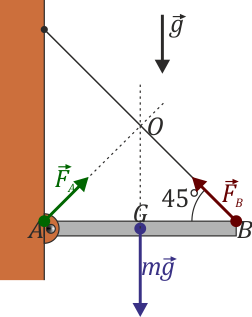
Archivo:barra-cable-tenso-03.png        Archivo:barra-cable-tenso-02.png

y que también lo es la suma de sus momentos. Esto se puede comprobar observando que las tres rectas soporte son concurrentes en un punto O. Si tomamos el momento respecto a dicho punto el resultados es nulo.

Obtenido de "http://tesla.us.es/wiki/index.php/Barra_sujeta_por_un_cable"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 16:04, 26 ene 2016. - Esta página ha sido visitada 4.512 veces. - Aviso legal - Acerca de Laplace