Leyes de conservación en polares y cilíndricas

De Laplace

(Diferencias entre revisiones)

Revisión de 13:51 28 nov 2015

Contenido

1 Enunciado
2 Fórmulas generales
3 Primer caso
4 Segundo caso

1 Enunciado

Una partícula de masa $m$ describe el movimiento expresado en cilíndricas

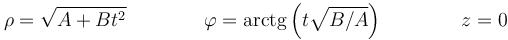
$\rho = \sqrt{A+Bt^2}\qquad\qquad \varphi = \mathrm{arctg}\left(t\sqrt{B/A}\right)\qquad\qquad z = 0$

Determine si se conserva la cantidad de movimiento, el momento cinético respecto al origen de coordenadas y la energía cinética. En su caso, halle el valor de las constantes.

Responda a las mismas preguntas para el movimiento helicoidal

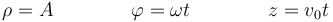
$\rho = A\qquad\qquad \varphi = \omega t\qquad\qquad z = v_0t$

2 Fórmulas generales

2.1 Cantidad de movimiento

La cantidad de movimiento de una partícula es el producto de su masa por su velocidad. La expresión de ésta, en coordenadas cilíndricas, es

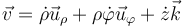
$\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\varphi}\vec{u}_\varphi+\dot{z}\vec{k}$

por lo que la cantidad de movimiento es

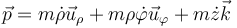
$\vec{p}=m\dot{\rho}\vec{u}_\rho+m\rho\dot{\varphi}\vec{u}_\varphi+m\dot{z}\vec{k}$

En el caso particular de movimiento en el plano OXY, la expresión se reduce a la de coordenadas polares

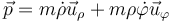
$\vec{p}=m\dot{\rho}\vec{u}_\rho+m\rho\dot{\varphi}\vec{u}_\varphi$

2.2 Momento cinético

$\vec{L}_O$ es igual al momento de la cantidad de movimiento, siendo el vector de posición en cilíndricas

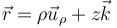
$\vec{r}=\rho\vec{u}_\rho+z\vec{k}$

por lo que resulta

$\vec{L}_O=\vec{r}\times\vec{p}=\left|\begin{matrix} \vec{u}_\rho & \vec{u}_\varphi & \vec{k} \\ \rho & 0 & z \\ \dot{\rho} & \rho\dot{\varphi} & \dot{z}\end{matrix}\right|=-mz\rho\dot{\varphi}\vec{u}_\rho+m(z\dot{\rho}-\rho\dot{z})\vec{u}_\varphi + \rho^2\dot{\varphi}\vec{k}$

En el caso de movimiento en el plano OXY el momento se reduce a

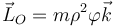
$\vec{L}_O=m\rho^2\varphi\vec{k}$

2.3 Energía cinética

La energía cinética, que es una cantidad escalar tiene una expresión más simple

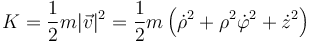
$K=\frac{1}{2}m|\vec{v}|^2=\frac{1}{2}m\left(\dot{\rho}^2+\rho^2\dot{\varphi}^2+\dot{z}^2\right)$

y en polares

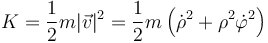
$K=\frac{1}{2}m|\vec{v}|^2=\frac{1}{2}m\left(\dot{\rho}^2+\rho^2\dot{\varphi}^2\right)$

3 Primer caso

El primer caso

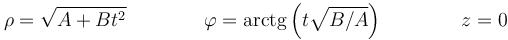
$\rho = \sqrt{A+Bt^2}\qquad\qquad \varphi = \mathrm{arctg}\left(t\sqrt{B/A}\right)\qquad\qquad z = 0$

es uno de movimiento plano, por lo que se pueden emplear coordenadas polares. A la hora de derivar, conviene observar que

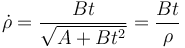
$\dot{\rho}=\frac{Bt}{\sqrt{A+B t^2}}=\frac{Bt}{\rho}$

y que

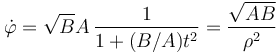
$\dot{\varphi}=\sqrt{B}{A}\,\frac{1}{1+(B/A)t^2}=\frac{\sqrt{AB}}{\rho^2}$

Estas dos relaciones permiten simplificar los cálculos que siguen.

3.1 Cantidad de movimiento

Sustituimos en la expresión de la cantidad de movimiento y queda

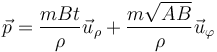
$\vec{p}=\frac{mBt}{\rho}\vec{u}_\rho+\frac{m\sqrt{AB}}{\rho}\vec{u}_\varphi$

Esta expresión parece que no es constante (aparece explícitamente t) pero hay que tener en cuenta que también $ρ$ y los vectores de la base dependen del tiempo.

La derivada de la cantidad de movimiento es igual a la fuerza, que en polares se expresa

$\vec{F}=m\left(\ddot{\rho}-\rho\dot{\varphi}^2\right)\vec{u}_\rho+m(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi})\vec{u}_\varphi$

Para la componente radial tenemos

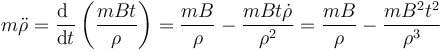
$m\ddot{\rho}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{mBt}{\rho}\right)=\frac{mB}{\rho}-\frac{mBt\dot{\rho}}{\rho^2}=\frac{mB}{\rho}-\frac{mB^2t^2}{\rho^3}$

y

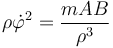
$\rho\dot{\varphi}^2 = \frac{m AB}{\rho^3}$

Restando estos dos términos

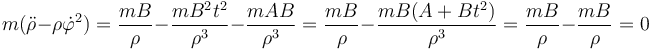
$m(\ddot{\rho}-\rho\dot{\varphi}^2)=\frac{mB}{\rho}-\frac{mB^2t^2}{\rho^3}-\frac{m AB}{\rho^3}=\frac{mB}{\rho}-\frac{mB(A+Bt^2)}{\rho^3}=\frac{mB}{\rho}-\frac{mB}{\rho}=0$

Es decir, la aceleración radial es nula en todo momento.

Para la acimutal tenemos

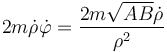
$2m\dot{\rho}\dot{\varphi}=\frac{2m\sqrt{AB}\dot{\rho}}{\rho^2}$

y

$\rho\ddot{\varphi}=\rho\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\sqrt{AB}}{\rho^2}\right)=-\frac{2\sqrt{AB}\dot{\rho}}{\rho^2}$

Si los sumamos

$F_\varphi=\frac{2m\sqrt{AB}\dot{\rho}}{\rho^2}-\frac{2m\sqrt{AB}\dot{\rho}}{\rho^2} = 0$

Por tanto, la componente acimutal de la fuerza también es nula en todo instante. Esto quiere decir que la fuerza, como vector, es nula en todo momento

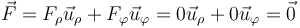
$\vec{F}=F_\rho\vec{u}_\rho+F_\varphi\vec{u}_\varphi = 0\vec{u}_\rho+0\vec{u}_\varphi=\vec{0}$

Si la fuerza es siempre nula, la cantidad de movimiento es una constante, aunque su expresión en polares parezca depender del tiempo.

3.2 Momento cinético

Si sustituimos en la expresión del momenti cinético en polares

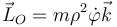
$\vec{L}_O=m\rho^2\dot{\varphi}\vec{k}$

nos queda simplemente

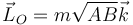
$\vec{L}_O=m\sqrt{AB}\vec{k}$

que es evidentemente constante, ya que el vector $\vec{k}$ lo es y la componente también.

Lo podíamos haber deducido igualmente de que la fuerza es nula en todo instante, ya que

$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O=\vec{r}\times\vec{F}=\vec{r}\times\vec{0}=\vec{0}$

3.3 Energía cinética

Por último, para la energía cinética tenemos

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): K=\frac{1}{2}m(\dot{\rho}^2+\rho^2\dot{\varphi}^2)=\frac{m}{2}\left(\frac{4B^2t^2}{\rho^2}+\frac{4AB}{\rho^2})=\frac{2mB(A+Bt^2)}{\rho^2}=2mB

que también es constante. De nuevo, podíamos haberlo demostrado partiendo de que la fuerza sobre la partícula es nula.

$\frac{\mathrm{d}K}{\mathrm{d}t}=\vec{F}\cdot\vec{v}=0$

3.4 Expresión en cartesianas

Podíamos haber demostrado que la fuerza sobre la partícula es nula en todo instante partiendo de la expresión en polares

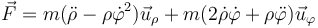
$\vec{F}=m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+m(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi})\vec{u}_\varphi$

hallando las derivadas “por fuerza bruta”.

Ahora bien, el que la fuerza sea nula en todo instante tiene la importante consecuencia de que el movimiento debe ser rectilíneo y uniforme. Sin embargo, no lo parece

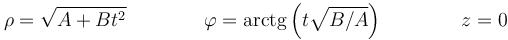
$\rho = \sqrt{A+Bt^2}\qquad\qquad \varphi = \mathrm{arctg}\left(t\sqrt{B/A}\right)\qquad\qquad z = 0$

Para ver que sí es un movimiento rectilíneo y uniforme pasamos a cartesianas. Tenemos que

$x = \rho\cos(\varphi)\qquad\qquad y=\rho\,\mathrm{sen}(\varphi)$

Aplicamos que

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \cos(\varphi)=\frac{1}{\sqrt{1+\mathrm{tg}^2(\varphi)} = \frac{\sqrt{A}}{\sqrt{A+Bt^2}}

y

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \mathrm{sen}(\varphi)=\frac{\mathrm{tg}(\varphi)}{\sqrt{1+\mathrm{tg}^2(\varphi)} = \frac{t\sqrt{B}}{\sqrt{A+Bt^2}}

y nos queda

$x = \sqrt{A+Bt^2}\frac{\sqrt{A}}{\sqrt{A+Bt^2}}=\sqrt{A}\qquad\qquad y = \sqrt{A+Bt^2}\frac{t\sqrt{B}}{\sqrt{A+Bt^2}}=t\sqrt{B}$

Por tanto el vector de posición es de la forma

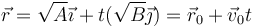
$\vec{r}=\sqrt{A}\vec{\imath}+t(\sqrt{B}\vec{\jmath})=\vec{r}_0+\vec{v}_0t$

que es naturalmente el de un movimiento rectilíneo y uniforme y por tanto se conservan la cantidad de movimiento, el momento cinético y la energía cinética, tal como se ve en otro problema.

4 Segundo caso

@@ Línea 107: / Línea 107: @@
 Si la fuerza es siempre nula, la cantidad de movimiento es una constante, aunque su expresión en polares parezca depender del tiempo.
+===Momento cinético===
+Si sustituimos en la expresión del momenti cinético en polares
+<center><math>\vec{L}_O=m\rho^2\dot{\varphi}\vec{k}</math></center>
+nos queda simplemente
+<center><math>\vec{L}_O=m\sqrt{AB}\vec{k}</math></center>
+que es evidentemente constante, ya que el vector <math>\vec{k}</math> lo es y la componente también.
+Lo podíamos haber deducido igualmente de que la fuerza es nula en todo instante, ya que
+<center><math>\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O=\vec{r}\times\vec{F}=\vec{r}\times\vec{0}=\vec{0}</math></center>
+===Energía cinética===
+Por último, para la energía cinética tenemos
+<center><math>K=\frac{1}{2}m(\dot{\rho}^2+\rho^2\dot{\varphi}^2)=\frac{m}{2}\left(\frac{4B^2t^2}{\rho^2}+\frac{4AB}{\rho^2})=\frac{2mB(A+Bt^2)}{\rho^2}=2mB</math></center>
+que también es constante. De nuevo, podíamos haberlo demostrado partiendo de que la fuerza sobre la partícula es nula.
+<center><math>\frac{\mathrm{d}K}{\mathrm{d}t}=\vec{F}\cdot\vec{v}=0</math></center>
+===Expresión en cartesianas===
+Podíamos haber demostrado que la fuerza sobre la partícula es nula en todo instante partiendo de la expresión en polares
+<center><math>\vec{F}=m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+m(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi})\vec{u}_\varphi</math></center>
+hallando las derivadas &ldquo;por fuerza bruta&rdquo;.
+Ahora bien, el que la fuerza sea nula en todo instante tiene la importante consecuencia de que el movimiento debe ser rectilíneo y uniforme. Sin embargo, no lo parece
+<center><math>\rho = \sqrt{A+Bt^2}\qquad\qquad \varphi =
+\mathrm{arctg}\left(t\sqrt{B/A}\right)\qquad\qquad z = 0
+</math></center>
+Para ver que sí es un movimiento rectilíneo y uniforme pasamos a cartesianas. Tenemos que
+<center><math>x = \rho\cos(\varphi)\qquad\qquad y=\rho\,\mathrm{sen}(\varphi)</math></center>
+Aplicamos que
+<center><math>\cos(\varphi)=\frac{1}{\sqrt{1+\mathrm{tg}^2(\varphi)} = \frac{\sqrt{A}}{\sqrt{A+Bt^2}}</math></center>
+y
+<center><math>\mathrm{sen}(\varphi)=\frac{\mathrm{tg}(\varphi)}{\sqrt{1+\mathrm{tg}^2(\varphi)} = \frac{t\sqrt{B}}{\sqrt{A+Bt^2}}</math></center>
+y nos queda
+<center><math>x = \sqrt{A+Bt^2}\frac{\sqrt{A}}{\sqrt{A+Bt^2}}=\sqrt{A}\qquad\qquad
+y = \sqrt{A+Bt^2}\frac{t\sqrt{B}}{\sqrt{A+Bt^2}}=t\sqrt{B}</math></center>
+Por tanto el vector de posición es de la forma
+<center><math>\vec{r}=\sqrt{A}\vec{\imath}+t(\sqrt{B}\vec{\jmath})=\vec{r}_0+\vec{v}_0t</math></center>
+que es naturalmente el de un movimiento rectilíneo y uniforme y por tanto se conservan la cantidad de movimiento, el momento cinético y la energía cinética, tal como se ve en [[Conservación en un movimiento rectilíneo y uniforme|otro problema]].
 ==Segundo caso==
 [[Categoría:Problemas de energía y leyes de conservación (GIE)]]

Leyes de conservación en polares y cilíndricas

De Laplace

Revisión de 13:51 28 nov 2015

Contenido

1 Enunciado

2 Fórmulas generales

2.1 Cantidad de movimiento

2.2 Momento cinético

2.3 Energía cinética

3 Primer caso

3.1 Cantidad de movimiento

3.2 Momento cinético

3.3 Energía cinética

3.4 Expresión en cartesianas

4 Segundo caso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES